معادلة شرودنغر والفلسفة الحتمية

الحمد لله تعالى وحده لا شريك له ولا ندَّ له، والصلاة والسلام على من بحبِّه لله لا مثيل له ولا نظير له. إنّ الهدف الأساسي الذي أنشده من خلال هذه السلسلة هو أن أبيِّن بعض المعالم الأساسية في ميكانيكا الكم، والتي يصعب أن نجد شرحاً لها بهذه الطريقة. وليس الهدف أن نعيد شرح هذه المواد كما في المناهج والكتب التي تركز على الجانب الرياضي من هذا العلم، فيخرج الطالب المتميز في الفيزياء بعدها خبيراً في الرياضيات، ولكن لا علم له من قريب أو بعيد بالمعاني الفيزيائية المتضمنة لها، والتي هي أهم من الجانب الرياضي.

في هذه الحلقة سنسلط الضوء على معادلة شرودنغر الموجية دون تفاصيل رياضية طويلة أو قصيرة، ولكن لنتعلم ماهيتها ومن أين جاءت، والمعاني الرياضية والفيزيائية المرافقة لها، ولنعرف ما هي التناقضات الفلسفية بينها وبين نتائجها من جهة، وبين الفيزياء الكلاسيكية والمبادئ الحتمية من جهة أخرى، ومن هنا نبدأ بحول الله.

تعريف عام بمعادلة شرودنغر الموجية

إنّ معادلة شرودنغر الموجية هي معادلة تفاضلية من الدرجة الثانية، وهذه المعادلة هي المكافئ الموجي الكوانتي لمبدأ حفظ الطاقة في الفيزياء الكلاسيكية، وتكتب هذه المعادلة على الصورة التالية:

ĤΨ = EΨ

حيثّ أنّ Ĥ يسمى بالهاملتونيان من الناحية الفيزيائية، وهو المؤثر التفاضلي للطاقة، ويطلق عليه رياضياً اسمEigen vector، أما E فهي طاقة النظام من الناحية الفيزيائية وهي مقدار ثابت، وتسمى رياضياً بالقيمة المميزة Eigen value. بالنسبة للمصطلح Eigen value فهو مركب من كلمتين، الأولى Eigen وهي كلمة ألمانية معناها مميز أو صحيح، والكلمة الثانية وهي value، ومعناها قيمة.

والهاملتونيان مكون من مجموع حدين: الأول هو حد تفاضلي من الدرجة الثانية والذي يمثل الطاقة الحركية، أما الحد الثاني فهو طاقة الوضع، وليس حداً تفاضلياً، وهو الذي باختلافه يختلف حل معادلة شرودنغر، وهو الذي يحدد مدى تعقيد الحل أو بساطته.

إنّ حل معادلة شرودنغر يعطي دالّة أو اقتراناً يمثِّل معادلة الموجة ويرمز له بالرمزΨ، والمعلومة التي يقدمها هذا الاقتران الناتج عن حل هذه المعادلة هي سعة الموجة.

ومع أنّ البعض يرى أنّه لا يوجدٌ معنى فيزيائياً وراء Ψ بحد ذاتها، إلا أنّ هذا الكلام قد لا يكون صحيحاً، فلو قالوا أنه لا توجد أهمية مباشرة ل Ψ لكان قولُهم أصح، وهي أيضاً غيرُ قابلة للقياس، أي أنها كمية نظرية بحتة، وهذا على خلاف الدالة الموجية الكلاسيكية، والتي يمكن قياسها مباشرةً.وقد جاءت معادلة شرودنغر من خلال تفاضل معادلة الموجة الجيبية الكلاسيكية المعلومة سلفاً وهي:

Ψ = A Sin (κ x – φ) , Equation of Sine wave

حيثُ أنّ κ هو العدد الموجي، وهو عبارة عن عدد الأمواج في مسافة مقدارها وحدة واحدة، لكن يبدو من خلال تعريفه الرياضي أنّ مقدار هذه الوحدة يساوي 2π، وبالمعادلات:

κ = 2 π/λ

و φ هو ثابت الطور، وهو ثابت تفاضلي اختياري لا يظهر في معادلة شرودنغر.

أما A فهو ثابت اختياري أيضاً لا يظهر في المعادلة التفاضلية، ويمثل أقصى سعة للموجة.

والحالة الموجية الثابتة التي على هذه الصورة، والتي هي الموجة الجيبية، هي حالة خاصة، حيثُ تكون طاقة الحركة وطاقة الوضع للموجة ثابتتين كل منهما على حدىً، لذلك فإنّ العدد الموجي لهذه الموجة سيكون ثابتاً، وسيعطي هذا طولاً موجياً ثابتا دائماً.

وهذه الموجة تمثل حالة موجيةً ثابتة كما أسلفنا، وتعميم المعادلة التفاضلية الناتجة عنها، لتشمل جميع الحالات الموجية – وليس فقط الموجات الجيبية – أنتج لنا ما يُعرف بمعادلة شرودنغر.وللمعلومة فإنّ أيّ اقتران رياضي يعطي معادلة تفاضلية واحدة له، والأمر ليس عشوائياً أو اختيارياً.

المعنى الرياضي لمعادلة شرودنغر

يعلم أيُّ شخص يعرف مبادئ التفاضل وخواص الاقترانات الرياضية أنّ المشتقة الثانية لأيِّ اقترانٍ رياضي تكشف عن تقعر ذلك الاقتران، فإذا كانت المشتقة الثانية موجبة، فإنّ الاقتران سيكون مقعراً لأعلى، أما إن كانت سالبة، فإنّ الاقتران سيكون مقعراً لأسفل.لكن عند النقطة التي تكون المشتقة الثانية تساوي الصفر، فإنّ هذه النقطة تكون نقطة انعطاف، وهي النقطة التي يتحول بعدها الاقتران مباشرةً من مقعر لأعلى إلى مقعر لأسفل، ولكن في تلك النقطة بالتحديد فإنّ الاقتران يكون في حالة حيادية من ناحية التقعر، لذلك فإنّ المماس عند تلك النقطة سيكون قاطعاً بلا شك.ننوه إلى أنّه يمكن كتابة معادلة شرودنغر على هذه الصورة:

Ψ” = – 2m/ħ² TΨ

حيثّ أنّ T هي الطاقة الحركية، والتي هي (E – V). ومن خلال هذه الصورة الأخيرة، فإنّ المشتقّة الثانية ل Ψ تتناسب مع سالب الطاقة الحركية ومع Ψ أيضاً.

إنّ هذا يعني أنّ التقعُّر يجب أن يكون دائماً باتجاه محور السينات، ولكن لماذا؟

ذلك أنّ الطاقة الحركية موجبة، وبوجود إشارة السالب، إن كانت Ψ موجبة (أي أنها فوق محور السينات) فإنّها يجب أن تكون مقعرة للأسفل، أي باتجاه المحور، لأنّ المشتقّة الثانية ل Ψ ستكون سالبة.

أما إن كانت Ψ سالبة (تقع تحت محور السينات) فإنّ المشتقّة الثانية ل Ψ ستكون موجبة، و سيكون الاقتران مقعراً للأعلى (أي باتجاه محور السينات أيضاً.

لذلك نجد دائماً أنّ التقعر في الموجات يكون باتجاه المحور كما يبين الشكل:

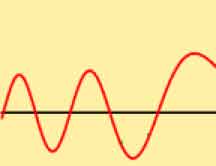
يظهر من هذا أن Ψ لا يمكن أن تدير ظهرها لمحور السينات ضمن هذه الفترة والتي هي فترة كلاسيكية.

لكن متى تساوي المشتقّة الثانية ل Ψ الصفر ؟

بالطبع فإنّ “Ψ ستساوي الصفر لأيّ نقطة انعطاف كما ذكرنا سابقاً، ولا يحدثُ هذا إلا أن تكون Ψ ذاتها مساوية للصفر، أو أنّ الطاقة الحركية تساوي الصفر، ويبدو هذا واضحاّ من خلال المعادلة الأخيرة.

أماΨ  فتساوي الصفر عندما تتقاطع هذه الدالة مع محور السينات، والشكل الأخير يوضح هذه الفكرة جيداً، ويمكن الملاحظة أنه عند أي نقطة التقاء بين Ψ ومحور السينات فإنّ هذه النقطة دائماً هي نقطة انعطاف، ويتضمن هذا أنّ سعة الموجة تساوي الصفر في تلك المنطقة.

أبرز المشكلات الفلسفية في معادلة شرودنغر من وجهة النظر الحتمية

من الوهلة الأولى فوجود معادلة حفظ الطاقة على هيئة معادلة تفاضلية، بدلاً من دالة رياضية متصلة رياضيا، سيسبب مشاكل نظرية كبيرة.وذلك أنّ حل هذه المعادلة التفاضلية سيحتمُ وضع شروط محددة ليكون الحل صحيحاً، لذلك كان علينا أن نشترط أنّ الطاقة لا بدّ أن تأخذ قيماً منفصلة (مكماة).

بينما في الميكانيكا الكلاسيكية، فإنّ الطاقة كمية متصلة، ولا يجوز أن تأخذ قيماً محددة، ولا وجود لقيم للطاقة غير مسموح بها.

هذه المشكلة بدت معالمها من الوهلة الأولى كما ذكرت، وقبل حل المعادلة، لكن هنالك مشاكل ستظهر بعد حلها أيضاً.

والمشكلة الثانية أنّ الدالة الموجية تتقاطع مع محور السينات أحياناُ عند نقاط الانعطاف كما ذكرنا، وهذا التقاطع سيجعل سعة الموجة عند تلك النقاط مساويةُ للصفر، مما يعني عدم وجود الجسيم الذي تمثله تلك الدالة في تلكم الأمكنة، بينما يتواجد حولها، بل ويعبر من تلك المنطقة التي يمكن وجوده فيها إلى المنطقة الأخرى التي يمكن أن يوجد فيها أيضاً، مارّاً في المنطقة التي بينهما دون أن يتواجد فيها.

والمشكلة الثالثة هي وجود الدّالة في أما كن مختلفة في ذات الوقت، ولأنّ وجود الدالة يعني وجود الموجة، وهذه الموجة قد تكون إلكتروناً مثلاً أو غيره، فهذا يعني أنّ الإلكترون يجب أن يكون موجوداً في عدة أماكن في وقت واحد، وهذا ما يتناقض مع الفطرة السليمة، وبالتالي مع الفيزياء الكلاسيكية، ومع الفلسفة الحتمية أيضاً.

لكن هذه المشاكل يمكن قبولها من الناحية الكلاسيكية، وذلك بأخذ التفسير الموجي للمادة، فلو قلنا من البداية أنّ الإلكترونات مثلاً هي أمواج، لما سببت لنا هذه النتائج قلقاً كبيراً.

لكنّ مصيبةً كوانتيةً ما زالت مخبأةً بعد، ولم تكشف عن نفسها للآن، وهذه المصيبة الكوانتية تكمن في أنّ الدالة الموجية تعطي قيماً في منطقة محرمة كلاسيكياً، فتتنبّأ بوجود الجسيمات الموجية في الفترة التي لا يمكن كلاسيكياً أن توجد فيها، وذلك لأنّ طاقتها الحركية تكون قد استنزفت بفعل طاقة الوضع قبل وصولها لها، أي أنها منطقة ذات طاقة حركية سالبة، وهذا ما يتناقض بالفعل مع الفطرة السليمة، ولا يمكن أن تقبل به الفيزياء الكلاسيكية تحت أي ظرف.

ويحدث هذا بسبب اختراق الدالة كما ذكرنا الحاجز الكلاسيكي عند النقطة التي تسمى نقطة الانقلاب الكلاسيكية، وهي إحدى نقاط الانعطاف، لأنّ الطاقة الحركية عندها تساوي الصفر، وقد أوضحنا أنّ نقاط الانعطاف توجد عندما تكون الدالة صفراً أو أنّ الطاقة الحركية تساوي الصفر.

وبعد نقطة الانعطاف هذه يتحول الاقتران من مقعر لأسفل باتجاه المحور الأفقي، إلى مقعر لأعلى، وهذه هي الحالة الوحيدة التي فيها تدير الدالة ظهرها لمحور السينات كما يبين الشكل:

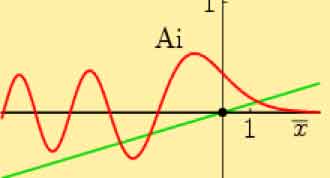
في الشكل الأخير يمثل المستقيم الأخضر طاقة الوضع، بينما يمثل محور السينات الطاقة الكلية، وهي مقدار ثابت كما هو ملاحظ.

وعند الخط العمودي الذي يظهر في الشكل فإنّ الطاقة الحركية تساوي الصفر، وتساوي طاقة الوضع الطاقة الكلية، والفترة الداخلية تسمى بالفترة الكلاسيكية كما في الشكل:

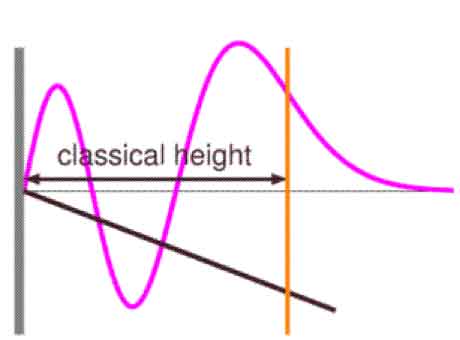
ويلاحظ كيف أنّ الدالة تنهار تماماً بعد هذا الخرق السافر للأعراف والقوانين التقليدية، لكي تصل الصفر بعد فترة ضئيلة نسبياً، حيثُ أنّ هذا الخرق لا يستمر طويلاً، فعلى الرغم من أنّ الميكانيكا الكوانتية اعتادت على مخالفة الفيزياء الكلاسيكية، إلا أنها أيضاً لا تفضل أن تتمادى كثيراً بذلك.

أود أن أطرح مثالاً لكي يتوضّح الأمر أكثر:

لو أنّنا قذفنا جسماً إلى أعلى بسرعة 10 م/ث، فإنّ هذا الجسم سيصل إلى أقصى ارتفاع وهو 5 م على اعتبار تسارع الجاذبية الأرضية 10 م/ث².

حسناً، لو قذفنا 1000 جسم بنفس تلك السرعة من نفس المكان، فلن تتغير النتيجة (أي أنّ النتيجة لن تتخلّف).

ولو قذفنا 10¹⁰ من الأجسام فلن تتغير النتيجة، ولن يتمكن أي من هذه الأجسام أن يتعدى حاجز الخمسة أمتار، ولن تكون هنالك فرصة لبعض هذه الأجسام من تعديها أو حتى عدم الوصول إليها، فالنتيجة معلومة محددة سلفاً.

هذه النقطة التي لا يمكن للأجسام أن تتعداها تسمى بنقطة الانقلاب الكلاسيكية، وهي النقطة التي تكون الطاقة عندها بالكامل على شكل طاقة وضع، والطاقة الحركية عندها تساوي الصفر.

بطبيعة الحال يختلف تعريف هذه النقطة من نظام لآخر، فقد لا تختفي الطاقة الحركية مطلقاً، فمثلاً في نظام كالمجموعة الشمسية، فإنّه توجد لكل كوكب نقطتي انعطاف هما الأوج والحضيض، وعند هاتين النقطتين تكون السرعة القطرية مساوية للصفر، أي أنّ الطاقة الحركية القطرية هي المساوية للصفر بينما الطاقة الحركية الزاوية ليست كذلك، وتبقى موجودة.

لنرجع لمثالنا، فحسب الميكانيكا الكوانتية هنالك احتمال واحد من ألف مثلاً أن تتجاوز بعض الأجسام المقذوفة بتلك السرعة حاجز الخمسة أمتار، لذلك سيكون لدينا جسم واحد من الألف سيجتاز ذلك الحاجز.وسيكون لدينا 10⁷ من ¹⁰10 سيجتاز ذلك الحاجز، وهذا كما ذكرت لكم لا يمكن أبداً قبوله ولا بأي تفسير كلاسيكي.

الأهمية الفيزيائية لحل معادلة شرودنغر

ذكرنا أنّ حل معادلة شرودنغر لأي نظام موجي يعطي صورة معادلة الموجة Ψ، وأنّ هذه الدالة تمثل سعة الموجة عند موضع معين.لكنّ الأهمية الفيزيائية من وراء Ψ لا تظهر إلا إذا وجدت Ψ مع مُرافقها الرياضي – ويرمز له بالرمز*Ψ –  لكي نوجد العناصر الاحتمالية للموجة صاحبة هذه الدالة.

إنّ أهمية الدالة الموجية الكوانتية في أنّ مربعها المطلق يعطي كثافة الاحتمال وليس الاحتمال لوجود الجسيم عند أي نقطة.

فيُعطى الاحتمال من خلال العلاقة التالية:

حيث أنّ dP هو احتمال وجود الجسيم في فترة مقدارها dx، ويمكن الحصول على احتمال وجود الجسيم ضمن أي فترة بإجراء التكامل على طرفي المعادلة الأخير بدلالة dx، حيث أنّ احتمال وجود الجسيم ضمن الفترة المعرفة عليها الدالة كاملة يساوي واحد. ويمكن الحصول على توقع أي كمية فيزيائية بوضعها بين الدالتين في المعادلة الأخيرة وإجراء التكامل على الفترة الصحيحة.وهنا تبرز مشكلةٌ فلسفيةٌ عميقة أيضاً، وهي أنّ هذه الدالة لا تعطي معلومات محددة لوجود للمادة، ولكنها تعطي معلومات ذات طابع احتماليٍّ لوجودها، وقد نوهنا أنّ الموجة تفترض وجود الجسيم الموجي على طول الفترة التي تتعرف عليها تلك الدالة، ولا تقوم فلسفتها على تحديد موقع الجسيم في موضع ما، وهذا كما سبق يمكن تعليله كلاسيكياً بوجود الخصائص الموجية للمادة.

لكن في الموجات الكلاسيكية فإنّ الاحتمالية تتمثل في Ψ  فقط وليس في مربعها المطلق، وهذا من الاختلاف بين الموجة الكلاسيكية والموجة الكوانتية.

الدالة الموجية لموجتين متراكبتين

أخيراً فإنّ الدوال الموجية قابلة للجمع، فإنه يمكن جمع دالتين موجيتين مختلفتين لينتج لدينا دالة جديدة ناتجة عن مجموعهما، وهذا يمكن عند تراكب موجتين معلومتي الدالتين، والتراكب يعني اختلاط الموجات وتداخلها.

ولكن لا يجوز أن نجمع الاحتماليات معاً، أي لا يجوز جمع مربعيهما مباشرة للحصول على الاحتمالية الناشئة عن تراكبهما، ولكن نربع الدالة الجديدة تربيعاً مطلقاً.

وهنا ننتهي بفضل الله من الجزء الرابع من هذه السلسلة التي أسأل الله تعالى أن ينفع بها، وانتظروا الجزء الخامس منها إن شاء الله. هذا والله أعلم، ولا تنسونا من صالح دعائكم

أ. مراد أبوعمر عضو منتدى الفيزياء التعليمي