في عالم الفيزياء كثيراً ما نسمع عن العالم أينشتاين ونيوتن وفراداي وغيرهم من أسماء الأعلام الشهيرة، الذين كان لهم دوراً هاماً في الانحراف العلمي، ولكن هناك ثنائي باحث على الرغم من عدم امتلاكهم لحالة الانحراف العلمي إلا أنهم قد تركوا بصمة مميزة في عالم الفيزياء، هما العالم تشارلز فابري (Charles Fabry) وألفريد بيروت (Alfred Perot).
قد كان العالم بيروت يعمل أستاذاً في جامعة مرسيليا، وفي عام 1894 قد تولى فابري منصب العالم بيروت في حين أصبح العالم بيروت أستاذاً للكهرباء الصناعية في هذه الجامعة، هنا كانت صدفة لقاء الثنائي! في ذلك الوقت قد كان فابري يدرس الدكتوراة في مجال خصائص حلقات التداخل، وقد كان بيروت قد درس دكتوراة في الديناميكا الحرارية ولكن قد حول اهتمامه بعد ذلك إلى تجارب الموجات الكهرومغناطيسية.
صدفة صنعت جهازاً
“الموضوع الذي بدأنا العمل فيه قد حدث لي، يمكن القول إنه عن طريق الصدفة، بعد ملاحظة في مشكلة كهربائية، حيث رغب فيزيائي شاب كان يعمل معي في دراسة تفريغ الشحنات (الشرارة) التي تمر بين الأسطح المعدنية المفصولة بمساحة صغيرة جداً بالميكرون أو أقل، استشارني حول الطريقة التي يمكنه استخدامها لقياس مثل هذه المسافات الصغيرة، وقد كنت على دراية بظاهرة التداخل وفكرت في الحال بأن طرق التداخل ستكون هي الحل الوحيد القادر على إعطاء الدقة المطلوبة” (تشارلز فابري).
من هنا بدأ الثنائي بالتفكير في طرق التداخل، إنها صدفة أخرى للقاء ولكن بطريقة أخرى فهنا قد التقت العقول لتعمل معاً، حتى توصلوا إلى جهاز يمكن من خلاله قياس التداخل، أطلق عليه اسم:
مقياس فابري-بيرو (Fabry -Perot Interferometers FPI) أو ايتالون (Etalon) أو دقة فابري – بيرو (Fabry-Perot Resolution).
قام الثنائي بنشر عدداً كبيراً من الأوراق حول مقياس التداخل الذي اخترعوه، وبين عامي 1896 و1902 قاما بنشر حوالي 15 مقالاً حول هذا المقياس، حيث تناولت أولى مقالاتهم المنشورة عام 1897 شرح نظرية مقياس التداخل وتطبيقها على القياس الدقيق للمسافات الصغيرة جداً بين الأسطح المعدنية المتوازية، بينما تناول المقال الثاني الذي نشر عام 1899 مخططاً تفصيلياً حول تركيب ووصف الجهاز وتطبيقه على التحليل الطيفي، حيث تمكن فابري من معالجة الجوانب النظرية لمقياس التداخل بينما قام بيروت بتصميم وبناء الجهاز.
ما هو مقياس فابري-بيرو!
الغرض منه: دراسة ظاهرة التداخل بين مكونات الضوء المختلفة حيث يعمل على تقوية الضوء عبر الانعكاسات المتعددة، ثم يحدث تداخل بناء بين مركباته ينتج عنه تحليل طيفي دقيق يمكننا من دراسة تركيب خطوط الطيفية للضوء بدقة وحساب الطول الموجي للضوء ومعرفة المسافة بين اللوحين العاكسين.
مكوناته: يتكون مقياس فابري-بيرو من:
- المصدر الضوئي.
- مرآتين متساويتين متوازيتين تعملان كعاكس جزئي حيث تبلغ انعكاسية كل منهما 95% (لوحين من الزجاج وجههما الداخلي من الفضة العاكسة)، المسافة بينهما (d) صغيرة جداً تقدر بوحدة المايكرومتر أو نانوميتر.
- عدسة محدبة لتجميع وتركيز الضوء النافذ الناتج عن الانعكاسات المتعددة على الشاشة.
- شاشة لتجميع الأشعة عليها والحصول على حلقات التداخل.
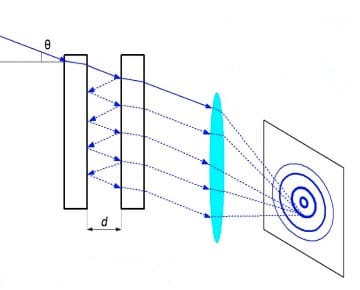
كيف يعمل؟
عندما يسقط الشعاع الضوئي من المصدر على المرآة الأولى بزاوية السقوط θ (الزاوية بين الشعاع الساقط والعمودي)، فإنه بناءً على قانون سنيل “Snell’s law ” الذي ينص على أن: عند انتقال الضوء من وسط ذو كثافة ضوئية أقل إلى وسط ذو كثافة ضوئية أكبر فإنه سينحرف مقترباً من العمودي ![]()
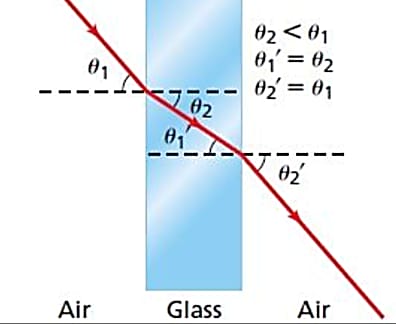
هذا يعني أن الشعاع الساقط من الهواء ذو الكثافة الضوئية الأقل إلى الزجاج ذو الكثافة الضوئية الأكبر، سوف ينحرف داخل الزجاج مقترباً نحو العمودي (أي أنه يحدث تغير في الطور)، ثم عند خروجه من الزجاج إلى الهواء نحو الفجوة بين المرآتين سوف ينحرف مبتعداً عن العمودي ويخرج بنفس زاوية سقوطه (θ) التي يسقط بها أيضاً على المرآة الثانية التي عندها ينقسم الشعاع إلى جزئين، الجزء الأكبر منه ينعكس داخل التجويف والجزء الآخر ينفذ من خلال المرآة.
الجزء الذي ينعكس يرتد متجهاً نحو المرآة الأولى ثم ينعكس عنها مرة أخرى نحو المرآة الثانية وينقسم إلى جزئين جزء ينفذ وجزء ينعكس وتستمر الانعكاسات على هذه الصورة.
بينما الجزء النافذ من الشعاع الناتج عن الشعاع الساقط و الأشعة المنعكسة سيمر من الهواء إلى الزجاج بحسب قانون سنيل ” Snell’s law” سوف ينحرف داخل الزجاج نحو العمودي ثم ينتقل من الزجاج إلى الهواء مبتعداً عن العمودي ليخرج بنفس زاوية سقوطه (θ)، ثم يسقط على العدسة المحدبة التي تقوم بتجميعه ليحدث تداخل للضوء وتركيزه على شاشة تظهر عليها الحلقات المضيئة والمعتمة، ويتضح ذلك في الشكل التالي:
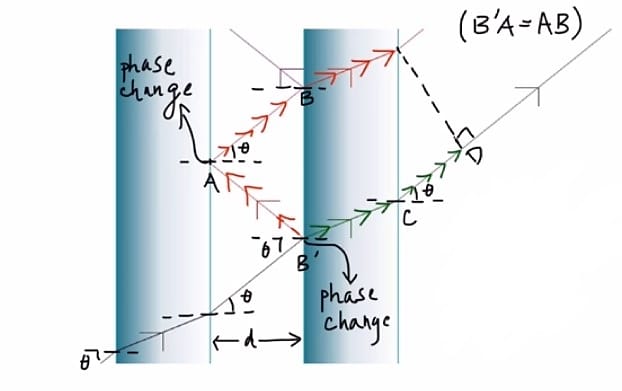
شروط حدوث التداخل هي:
- Coherent light أن تكون الموجات مترابطة أي أن يكون فرق الطور في أي لحظة ثابت.
- Monochromatic light أن تكون الموجات أحادية الطول الموجي ، لها نفس التردد (أحادية اللون).
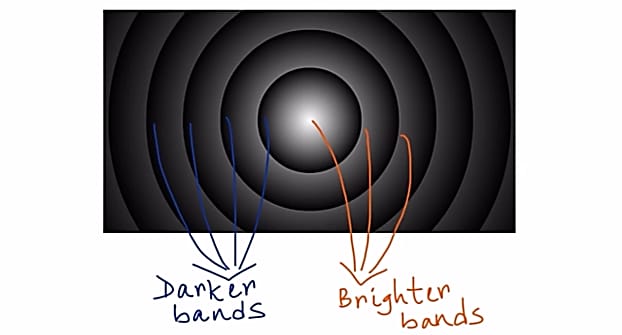
الحلقات الناتجة تتكون من:
- هدب مضيئة: تظهر نتيجة حدوث تداخل بناء
- يكون عندها فرق المسار عدد صحيح من الأطوال الموجية كما في الشكل:
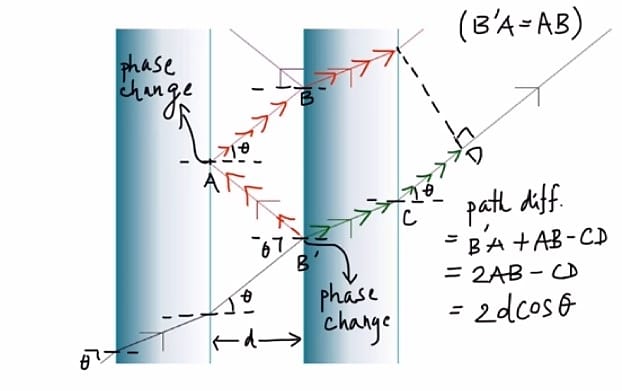
معادلة التداخل البناء هي:
![]() حيث أن:
حيث أن:
d: المسافة الفاصلة بين المرآتين، : n رتبة التداخل ، θ: زاوية السقوط ، ϻ : معامل الوسط (الهواء) =1 .
فإن معادلة التداخل البناء تصبح:
![]()
- هدب معتمة: تظهر نتيجة حدوث تداخل هدام.
- يكون عندها فرق المسار عدد صحيح من أنصاف الأطوال الموجية.
- معادلة التداخل الهدام هي:
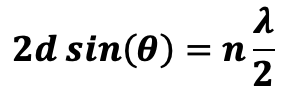
الشكل التالي يوضح الفرق بين التداخل البناء والتداخل الهدام:
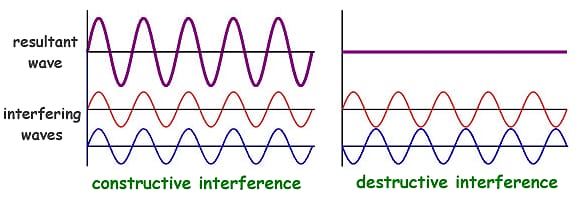
في هذه التجربة يتم متابعة الهدب المضيئة الناتجة عن التداخل البناء حيث يتم من خلالها حساب التالي:
- في حالة معرفتنا للمسافة بين المرآتين (d)، وزاوية سقوط الشعاع (θ):
يمكننا حساب الأطوال الموجية المنبعثة من المصدر الضوئي ![]()
- في حالة معرفتنا للطول الموجي (λ) ومقدار زاوية السقوط (θ)
يمكننا حساب المسافة بين المرآتين (البعد بين اللوحين الزجاجيين) ![]()
إذا قمنا بتغيير البعد بين المرآتين في مقياس التداخل سنلاحظ أن الحلقات تتحرك بالتناوب كما في الشكل

في حالة تغيير المسافة بين المرآتين يسمى الجهاز حينها باسم “Etalon” أما في حالة المسافة ثابتة بين المرآتين يسمى عندها “Fabry- Perot Interferometer”.
من الفائز؟
عندما تقارن بين صورتين قد التقطتهما كاميرتين مختلفتين أول ما تنظر إليه هو الجودة والدقة فالصورة ذات الدقة الأعلى ستجعلك تحكم بأن الكاميرا التي التقطتها هي الأفضل، وكذلك بالنسبة لمقياس فابري- بيرو، قبل اكتشاف مقياس فابري-بيرو كان هناك العديد من المقاييس المستخدمة للتداخل، كمقياس مايكلسون ومقياس حلقات نيوتن، لكن عند ظهور مقياس فابري-بيرو قد تفوق على تلك المقاييس التي كانت تستخدم حينها فقد كان هو ملك عصره، ما الذي يميزه ليكسب الحكم!
لو حاولنا أن نقارن بين نمط التداخل الناتج عن مقياس مايكلسون ونمط التداخل الناتج عن مقياس فابري-بيرو، سنجد أن مقياس تداخل مايكلسون ينقسم الضوء في داخله إلى شعاعين ، أحدهما يتأخر بمسافة 2d عن الآخر، ثم يتداخلان معاً فينتج حلقات مايكلسون، أما في مقياس فابري-بيرو ينقسم الضوء إلى عدد كبير من الأشعة التي تتأخر بشكل كبير حيث أنها تنعكس انعكاسات عديدة التي ينتج عنها حلقات ضيقة، حيث أنها تمتاز عن حلقات مايكلسون بأنها أكثر حدة فهي تعطي قياسات أكثر دقة من حلقات مايكلسون ، وهذا ما جعل مقياس فابري-بيرو هو الفائز وذلك بحكم دقته العالية جداً الناتجة عن الانعكاسات العديدة . انظر إلى الشكل التالي ستلاحظ الفرق في الحدة بين الحلقات.
 |
 |
| حلقات فابري-بيرو | حلقات مايكلسون |
 |
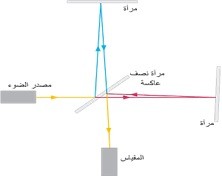 |
| مقياس فابري -بيرو | مقياس مايكلسون |
تقاس الدقة لمقياس فابري -بيرو (R) من خلال القانون
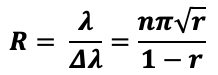
حيث أن:
n : هي رتبة التداخل ≈![]() عند زاوية السقوط الصغيرة.
عند زاوية السقوط الصغيرة.
: r انعكاسية سطح ايتالون .
هذا يعني بأن أقل فصل بين الطولين الموجيين لخطين الطيف يتم الحصول عليه من القانون
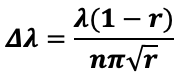
يعني هذا الفصل بأن الطولين الموجيين يحققان معيار رايلي.
إذا نستنتج أن مقياس تداخل فابري-بيرو يمتاز بأن نطاق الطيف من الأطوال الموجية غير محددة وأن نتيجة التغير في الطول الموجي يحدث إزاحة للحلقات الناتجة وفق العلاقة التالية:
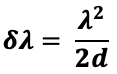
وهذا ما يجعل مقياس فابري- بيرو ذو دقة عالية.
بعض التطبيقات التي يستخدم فيها مقياس فابري-بيرو:
- يستخدم في الليزر حيث يساعد على تحديد الطول الموجي لضوء الليزر.
- يستخدم في الفلك حيث يساعد الفلكيين على تحديد التركيب الكيميائي للنجوم البعيدة ودراسة حركة المجرات.
- يستخدم في دراسة تركيب الذرة حيث أنه في الفترة ما قبل ظهور علم فيزياء الكم قد كانت أفضل وسيلة لهذه الدراسات هي التحليل الطيفي للضوء المنبعث من الذرة، حيث أن كل نوع من الذرات يشع مجموعة من الترددات تسمى الخطوط الطيفية المميزة لكل ذرة.
- يستخدم في شبكات الاتصالات، ففي عام 2005 بدأت بعض شركات الاتصالات باستخدام (etalons) مقياس فابري-بيرو ثابت المسافة بين العاكسين.
- يستخدم في صناعة مرشحات ثنائية اللون التي تتواجد في الكاميرات والمعدات الفلكية وأنظمة الليزر التي تعمل على عكس الأطوال الموجية الغير مرغوب فيها.
- يستخدم داخل مرنان الليزر حيث يساعد على تغيير وضع تشغيل الليزر من multi mode إلى single mode .
- صنع مطياف قادر على مراقبة تأثير زيمان.
- الكشف عن أمواج الجاذبية حيث يتم باستخدام تجويف فابري-بيرو لتخزين الفوتونات لمدة مللي ثانية أثناء ارتدادها للأعلى وللأسفل بين المرايا مما يزيد من الوقت الذي يمكن أ تتفاعل فيه موجة الجاذبية مع الضوء مما يؤدي إلى حساسية أفضل عند الترددات المنخفضة.
- التحكم في الأطوال الموجية للضوء وقياسها.






