مخططات فاينمان

نتيجة لتراكم النتائج التجريبية فقد دخلت ميكانيكا الكم الى مرحلة جديد حيث اصبحت الطرائق الحسابية المعروفة ميوؤس منها وغير كافية للتعامل مع تعقيدات النظرية. وفي عام 1948 إقترح ريتشارد فاينمان طريقة جديدة أدت الى تبسيط هائل، حيث تعتمد طريقته اعتماداً كبيراً على اجراء عدد قليل نسبياً من الرسوم وهي الان اصبحت تُعرف بمخططات فاينمان، فمثلاً إذا كانت لدينا حالة فيزيائياً مُعينة فاننا نقوم برسم عدد قليل من هذه المخططات ومن ثم نقوم بتطبيق قواعد بسيطة ترتبط بهذه الرسوم لنحصل على الاجابات الحسابية بصورة مباشرة، ونسبة لبساطة وقوة هذه الطريقة فقد اصبحت تمثل الاداة الاساسية لاجراء الحسابات في فيزياء الجسيمات الاولية.
قواعد فاينمان
لقد اصبحت قواعد فاينمان هي الاداة الاساسية التي يستخدمها فيزيائي الجسيمات الاولية المعاصرين. وهذه القواعد تشتمل على المفاهيم الاساسية لميكانيكا الكم والشئ المهم والرائع هو انها يمكن تمثيلها في صورة مُخططات، ولكي نقدر قدر هذه المخططات فاننا نحتاج الى فهم عدد قليل من المفاهيم الاساسية.
في مخططات فاينمان يتم تمثيل الجسيمات عن طريق خطوط مستقيمة ويتم تمثيل التفاعلات بين الجسيمات عن طريق النقاط التي تتقابل فيها هذه الخطوط ونقطة التفاعل تعرف بالفيرتكس التي معناه ركن او رأس، ويناط بكل مخطط كمية مُعينة ممايجعل مخططات فاينمان وسيلة لاتقدر بثمن في اجراء الحسابات في ميكانيكا الكم.
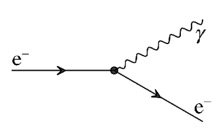 المثال البسيط والاكثر وضوحاً هو تفاعل الالكترونات مع الفوتونات وهو التفاعل الذي نراه بشكل دائما بما تحمل الكلمة من معنى، اي عندما ينبعث الضوء من الالكترونات وبلغة مخططات فايمان يتم تمثيل الاكترون بخط به سهم يتشعب منه خط متعرج يمثل الفوتون، والسهم هنا لايمثل اتجاه الحركة بل يمثل اتجاه تدفق الشخنة الكهربية السالبة.
المثال البسيط والاكثر وضوحاً هو تفاعل الالكترونات مع الفوتونات وهو التفاعل الذي نراه بشكل دائما بما تحمل الكلمة من معنى، اي عندما ينبعث الضوء من الالكترونات وبلغة مخططات فايمان يتم تمثيل الاكترون بخط به سهم يتشعب منه خط متعرج يمثل الفوتون، والسهم هنا لايمثل اتجاه الحركة بل يمثل اتجاه تدفق الشخنة الكهربية السالبة.
تفاعل الضوء مع الالكترونات معروف منذ وقت طويل، ولذلك فانه لدينا فهم دقيق للفيزياء التي يصفها هذا المخطط، ومع ذلك فيجب ان نعلم ان هذه المخططات تنطبق على الكثير من الحالات والفرق بين حالة واخرى يكمن في كل التشكيلات الابتدائية والنهائية الممكنة، وهذه هي طبيعة ميكانيكا الكم فنحن عادة ما نُحدد الحالات الابتدائية والنهائية وميكانيكا الكم تقدم لنا قيمة الاحتمال لحدوث العملية اي احتمال الانتقال من الحالة الابتدائية الى الحالة النهائية. وبالتالى ومن الناحية العملية يجب ان يُلحق بالمخطط الحالات الابتدائية والنهائية للعملية، فمثلاً نجد في الكثير من الامثلة ان الحالة الابتدائية تمثلها الجسيمات القادمة من المعجلات بينما ان الحالة النهائية تمثلها الجسيمات الصادرة التي يتم رصدها في كاشف الجسيمات، وبتعبير آخر فان الحالة الابتدائية هي الجسيمات المتحركة بحرية قبل عملية التصادم بينما ان الحالة النهائية هي الجسيمات الخارجة من التصادم. ومع ذلك فان هناك حالات اخرى كثيرة يصفها نفس المخطط اعلاه، فعلى سبيل المثال من المحتمل ان يكون الالكترون في الحالة الابتدائية في المخطط اعلاه هو الكترون في مدار ذو طاقة عالية في ذرة ما ثم سقط الى مدار له طاقة ادني فنبعث فوتون طاقته تساوي الفرق بين طاقتي المداريين.
الدرس المهم الذي يجب ان نتعلمه من هذا المخطط هو ان الجسيمات يمكن ان تنشأ في عملية التفاعل، ففي الحالة الابتدائية لم يكن الفوتون موجوداً اصلاَ وفي اللحظة التالية دخل الفوتون الى حيز الوجود.
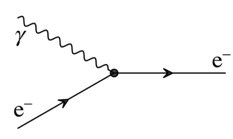 الان يمكننا ان نتحدث عن الحالة العكسية اي عندما نقوم بتحويل الفوتون من الحالة الابتدائية الى الحالة النهائية اي عندما يقوم الالكترون بامتصاص الفوتون مثلما يحدث عملياً في حالة سقوط الفوتون على العين فتمتصه الالكترونات التي بدورها تعمل على اثارة العصب البصري. عملية تحويل الجسيم من كونه جسيم داخل الى التفاعل الى جسيم صادر من التفاعل (او العكس) تمثل خاصية مهمة تتمتع بها مخططات فاينمان حيث ان عملية التحويل هذه ينتج عنها مخطط جديد يقابل عملية تفاعل اخرى مُحتملة الحدوث مما يفتح المجال امام امكانية اخرى كثيرة.
الان يمكننا ان نتحدث عن الحالة العكسية اي عندما نقوم بتحويل الفوتون من الحالة الابتدائية الى الحالة النهائية اي عندما يقوم الالكترون بامتصاص الفوتون مثلما يحدث عملياً في حالة سقوط الفوتون على العين فتمتصه الالكترونات التي بدورها تعمل على اثارة العصب البصري. عملية تحويل الجسيم من كونه جسيم داخل الى التفاعل الى جسيم صادر من التفاعل (او العكس) تمثل خاصية مهمة تتمتع بها مخططات فاينمان حيث ان عملية التحويل هذه ينتج عنها مخطط جديد يقابل عملية تفاعل اخرى مُحتملة الحدوث مما يفتح المجال امام امكانية اخرى كثيرة.
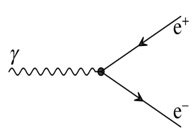 وإذا قمنا مثلاً بعكس اتجاه السهم في خط الالكترون الداخل للتفاعل في مخطط فاينمان فان النتيجة سوف تُعطي فوتون داخل ينتج عنه زوج من الالكترونات.
وإذا قمنا مثلاً بعكس اتجاه السهم في خط الالكترون الداخل للتفاعل في مخطط فاينمان فان النتيجة سوف تُعطي فوتون داخل ينتج عنه زوج من الالكترونات.
بالنظر للاسهم نلاحظ ان احد الالكترنين في الزوج الصادر عن التفاعل، له سهم معكوس الاتجاه ولكن وكما قلنا سابقاً ان اتجاه السهم في مخطط فاينمان يشير الى اتجاه تدفق الشحنة الكهربية السالبة ولذلك فان خط الالكترون الذي به سهم معكوس الاتجاه يمثل جسيم يشبه تماماً الالكترون في كل شئ الا ان شحنته الكهربية موجبة وهذا الجسيم يطلق عليه اسم البوزيترون وهو الجسيم المُضاد للالكترون وقد تم اكتشافه عملياً في عام 1932 بواسطة كارل د. اندرسون.
الان لدينا قاعدة من قواعد فاينمان تنص على: عندما يكون لدينا جسيم صادر من نقطة التفاعل وكان السهم في خط هذا الجسيم يشير الى الداخل (نحو نقطة التفاعل) فاننا نفسر هذا الجسيم على انه جسيم له شحنة كهربية مُضادة. وعملية تبديل خط الجسيم من جسيم داخل للتفاعل الى جسيم صادر عن التفاعل (او العكس) تبدل الجسيم الى جسيم مُضاد (او العكس).
قوانين انحفاظ الطاقة وكمية التحرك
عملية التفاعل يجب ان تخضع لقوانين انحفاظ الطاقة وكمية التحرك. فمثلاً نجد ان الالكترون في الذرة يستطيع ان يشع فوتوناً شريطة ان ينتقل من مستوى طاقة اعلى الى مستوى طاقة أدنى، ولكن الالكترون الساكن عن الحركة اي الذي كمية تحركه تساوي صفراً يكون في مستوى الطاقة الادني له، وعليه لو قام هذا الالكترون باشعاع فوتون فانه يجب ان ينتقل الى مستوى طاقة ادنى من مستوى طاقته قبل الاشعاع وهذا طبعاً مستحيل لان الالكترون اصلاً كان في ادنى مستوى طاقة ممكن، لذلك فان الالكترون الساكن من المستحيل ان يشع فوتوناً. ونفس هذ الامر ينسحب على الاكترون الحر اي الالكترون المتحرك بسرعة ثابتة في خط مستقيم والسبب انه يوجد مراقب ما (يتحرك بنفس السرعة وفي نفس الاتجاه) بالنسبة له هذا الالكترون يُعتبر ساكناً عن الحركة وعليه فان عملية إطلاق الفوتون بوسطة هذا الالكترون مستحيلة الحدوث بالنسبة لهذا المراقب والقاعدة العامة تقول إذا كان حدوث العملية مستحيل بالنسبة لمراقب ما فانها مستحيلة الحدوث بالنسبة لجميع المراقبين.
ايضاً نجد ان الفوتون المتحرك في الفضاء الحر لايمكن ان يصدر عنه الزوج من الالكترون والبوزيترون حتى ولو كان لهذا الفوتون طاقة عالية جداً والسبب هو انه يوجد دائماً مراقب ما بالنسبة له هذا فوتون يُعتبر فوتون ذو طاقة منخفضة (طاقته اقل من مجموع طاقتي السكون للالكترون والبوزيترون). طبعاً نحن نعلم ان الفوتون يتحرك بسرعة الضوء ممايعني ان سرعته تظل ثابتة بالنسبة لجميع المراقبين ولن يستطيع اي مراقب ان يلحق بالفوتون ولكن نتيجة للتأثير الازحي نحو الاحمر (زيادة الطول الموجي نتيحة للسرعة النسبية) فان الفوتون ذو الطاقة العالية قد يبدو للمراقب المتحرك بسرعة عالية (في نفس اتجاه حركة الفوتون) مزاحاً في طوله الموجي نحو الاحمر اي ان طوله الموجي يزداد وبالتالي طالما ان طاقة الفوتون تتناسب عكسياً مع الطول الموجي فان هذا الفوتون يعتبر فوتوناً ذو طاقة منخفضة وليس بمقدوره ان يشع الزوج الالكترون-بوزيترون. ولكن وفي حالة وجود جسيم آخر يقوم باضافة او إمتصاص جزء من الطاقة والاندفاع فان عملية إنتاج الزوج ممكنة الحدوث. فمثلاً في حالة اصطدام مع الانوية فان الفوتون ذو الطاقة العالية يستيطع ان يصدر الزوج الالكترون-بوزيترون، وعلى الرغم من المراقب المتحرك في نفس اتجاه الفوتون يرى ان للفوتون طاقة منخفضة فان حركة المراقب نفسها تجعل من النواة متحركة بسرعة كبيرة حسب مناطه الاسنادي، وعليه فان تصادم الفوتون مع النوة سوف يمد الفوتون بطاقة كافية تسمح له بانتاج الزوج الكترون-بوزيترون. والمخطط ادناه يمثل عملية إنتاج الفوتون للزوج في وجود نواة (الخط العريض في المخطط) ثقيلة.
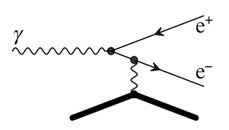
الجسيمات الظاهرية
يمكن للجسيمات ان تحمل طاقة “مرفوضة” شريطة ان يحدث ذلك لفترة زمنية وجيزة جداً، وكلما زاد مقدار الطاقة “المروفضة” كلما صغُرت الفترة الزمنية (مبدأ الارتياب في قياس الطاقة والزمن) وما نعنيه بالطاقة المرفوضة هي اي طاقة يختلف مقدارها عن القيمة التي تأخذها الطاقة بناءاً على مقدار كمية الحركة، مثلاً نعلم ان الالكترون الساكن عن الحركة له طاقة تسمى بالطاقة السكونية ومقدار هذه الطاقة السكونية يساوي حاصل ضرب الكتلة في مربع سرعة الضوء وعليه فليس من المقبول ان تكون طاقة الالكترون الكلية تساوي صفراً، ولكن وعلى الرغم هذا فإن ميكانيكا الكم تسمح بوجود الكترونات لها طاقة تساوي الصفر او حتى طاقة سالبة او طاقة عالية جداً بصورة غير معقولة (مثلاً الكترون ساكن يحمل طاقة عالية جداً جدا!!ً) شريطة ان يحدث ذلك في زمن وجيز جداً. و على وجه الخصوص وعلى ضوء المناقشة السابقة فانه يمكن للفوتون ان يتحول لحظياً الى زوج الالكترون- البوزيترون ثم بعد فترة زمنية صغيرة جداً يتحد هذا الزوج ليصبح فوتوناً مرة آخرى، والمخطط التالي يوضح هذه الامكانية.
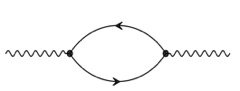
وكل جسيم يحمل طاقة او كمية تحرك مرفوضة نطلق عليه إسم جسيم ظاهري والجسيمات الظاهرية هي جسيمات غير حقيقية تنشأ في مرحلة وسيطة اثناء عملية اجراء الحسابات الرياضياتية في مخططات فاينمان وهذه الجسيمات الظاهرية لايمكن رصدها بصورة مباشرة شأنها شأن الفوتونين في تجربة يونج للشق المذدوج، التي تتحرك من المصدر الضوئي الى الشاشة (الحائل) وأذا طرحنا السؤال: ماهو الشق الذي عبر من خلاله الفوتون عند انتقاله من المصدر الى الشاشة؟ فانه وفقاً لفلسفة ميكانيكا الكم، ليس لهذا السؤال اي معنى ومن المستحيل الاجابة عليه.
اذن يمكن للفوتون ولزمن وجيز جداً ان ينتج زوج ظاهري الالكترون-البزيترون وهذا الامر تترتب عليه نتائج اخرى، فمثلاً لو سمحناً لفوتون آخر ان يعبر مسار الفوتون الاول اثناء وجوده في حالة الانفصال (الكترون-بوزيترون) فانه يمكن ان يتم إمتصاص هذا الفوتون بواسطة احد جسيمات الزوج الظاهري وان يتم اطلاقه بواسطة الجسيم الاخر والمخطط التالي يوضح هذه العملية.
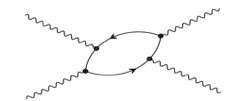
نحن نعلم بالضبط قيمة ثابت الاقتران للالكترون مع فوتون (المخططات السابقة) ونعرف الخصائص الكمومية للالكترونات والفوتونات ولذلك فاننا نستطيع حساب إحتمال حدوث العملية اعلاه، والتي يمكن رصدها تجريبياً في صورة تشتت للضوء بواسطة الضوء وعلى الرغم من ضعف هذا التأثير الا انه قد تم بالفعل رصده تجريبياً.
هذا التأثير يشبه ما يُعرف بالتأثير النفقي في ميكانيكا الكم. حيث يستطيع الجسيم ان يعبُر حاجزاً للطاقة حتى ولو لم يكن لهذا الجسيم الطاقة الكافية لبلوغ قمة الحاجز، فالالكترون مثلاً يمكنه ان يعبُر الجبل حتى ولو لم يكن لهذا الالكترون طاقة كافية لبلوغ قمة الجبل، فهو قد يمر من خلال نفق مخترقاً الجبل. وإذا كان الالكترون في البداية في أحد جانبي النفق ثم في النهاية اصبح الالكترون عند الجانب الاخر للنفق، فمن الطبيعي ان نقول ان “الالكترون قد عبر من خلال النفق” ولكن هذه المقولة تقع خارج حدود ميكانيكا الكم أذ انه لاتوجد اي امكانية لتحديد ما اذا كان الالكترون قد توجد عند منتصف الطريق في الجبل، والالكترون داخل النفق يعتبر الكترون ظاهري، ولو اجرينا تجربة لتحديد موقع الالكترون فان التأثير النفقي نفسه سوف يختفي تماماً. اذن بالمعنى البديهي فإن الالكترون قد مر من خلال النفق الا ان اي محاولة لرصد الالكترون داخل النفق سوف تبؤ بالفشل وكل مانستطيع رصده هو الحالة الابتدائية (الالكترون عند أحد جانبي النفق) والحالة النهائية (الالكترون عند الجانب الاخر للنفق) ولكن لن نستطيع ابداً ان نرصد الجسيمات الظاهرية الوسيطية (الالكترون داخل النفق).
هناك تأثير اخير نريد ان نناقشه هنا وهو التداخل. فنحن نعلم ان الضوء يتداخل مع نفسه، ولكن ايضاً نجد ان الجسيمات بدورها تحمل نفس هذه الخاصية، فمثلاً إذا كانت لدينا حالة مُعينة وتوجد أكثر من طريقة واحدة للانتقال من الحالة الابتدائية الى الحالة النهائية، فان الامكانيات المختلفة للانتقال من الحالة الابتدائية الى الحالة النهائية تتداخل مع بعضها البعض اما تداخلاً هداماً او بناءاً. وعند اجراء الحسابات فإن النظريين يقومون برسم كل المخططات المختلفة الممكنة (اي المخططات التي لها نفس التشيلات الابتدائية والنهائية) ثم يكتبون التعابير الرياضياتية المصاحبة لهذه الامكانيات المختلفة ويقومون بجمج او طرح (التداخل البناء والتداخل الهدام) المساهمات المختلفة ومربع المجموع الكلي لهذه المساهمات سوف يعطي الاحتمال الكلي لحدوث العملية المُعينة. فمثلاً لحساب احتمال تشتت الضوء بواسطة الضوء نحتاج ان نرسم ستة مخططات تمثل الامكانيات المختلفة، ونقوم بدمج مساهمات كل هذه المخططات لنحصل على الاحتمال الكلي، والمخططات ادناه تبين كل الامكانيات المختلفة الممكنة للعملية.
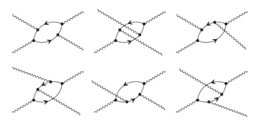
وكل مخطط من هذه المخططات يمثل امكانية مُحددة ومساهمته اما ان تكون موجبة او تكون سالبة والمساهمات سوف تتداخل مع بعضها البعض، وبأخذ المجموع الكلي وايجاد المربع نحصل على احتمال حدوث عملية التشتت. وابداً لن يستطيع أحد ان بداعي ان واحد من بين هذه المخططات دون غيره قد حدث بالفعل. لان هذا الادعاء سوف يكون بمثابة السؤال عن الشق الذي عبر من خلاله الفوتون في تجربة الشق المزدوج.