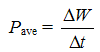محاضرة 9 فيزياء عامة (1) ميكانيكا نيوتن .. الشغل والطاقة
إن مفهوم الشغل والطاقة مهم جداً في علم الفيزياء، حيث توجد الطاقة في الطبيعة في صور مختلفة مثل الطاقة الميكانيكية Mechanical energy، والطاقة الكهرومغناطيسية Electromagnetic energy، والطاقة الكيميائية Chemical energy، والطاقة الحرارية Thermal energy، والطاقة النووية Nuclear energy. إن الطاقة بصورها المختلفة تتحول من شكل إلى آخر ولكن في النهاية الطاقة الكلية ثابتة. فمثلا الطاقة الكيميائية المختزنة في بطارية تتحول إلى طاقة كهربية لتتحول بدورها إلى طاقة حركية. ودراسة تحولات الطاقة مهم جداً لجميع العلوم.
 وفى هذا الجزء من المقرر سوف نركز على Mechanical energy. وذلك لأنه يعتمد على مفاهيم القوة التي وضعها نيوتن في القوانين الثلاثة، ويجدر الذكر هنا أن الشغل والطاقة كميات قياسية وبالتالي فإن التعامل معها سيكون أسهل من استخدام قوانين نيوتن للحركة، وذلك لأننا كنا نتعامل وبشكل مباشر مع القوة وهى كمية متجهة. وحيث أننا لم نجد أية صعوبة في تطبيق قوانين نيوتن وذلك لأن مقدار القوة المؤثرة على حركة الأجسام ثابت، ولكن إذا ما أصبحت القوة متغيرة وبالتالي فإن العجلة ستكون متغيرة وهنا يكون التعامل مع مفهوم الشغل والطاقة اسهل بكثير في مثل هذه الحالات.
وفى هذا الجزء من المقرر سوف نركز على Mechanical energy. وذلك لأنه يعتمد على مفاهيم القوة التي وضعها نيوتن في القوانين الثلاثة، ويجدر الذكر هنا أن الشغل والطاقة كميات قياسية وبالتالي فإن التعامل معها سيكون أسهل من استخدام قوانين نيوتن للحركة، وذلك لأننا كنا نتعامل وبشكل مباشر مع القوة وهى كمية متجهة. وحيث أننا لم نجد أية صعوبة في تطبيق قوانين نيوتن وذلك لأن مقدار القوة المؤثرة على حركة الأجسام ثابت، ولكن إذا ما أصبحت القوة متغيرة وبالتالي فإن العجلة ستكون متغيرة وهنا يكون التعامل مع مفهوم الشغل والطاقة اسهل بكثير في مثل هذه الحالات.
ولكن قبل أن نتناول موضوع الطاقة فإننا سوف نوضح مفهوم الشغل الذي هو حلقة الوصل ما بين القوة والطاقة.
والشغل قد يكون ناتجاً من قوة ثابتة constant force أو من قوة متغيرة varying force. وسوف ندرس كلا النوعين في هذا الفصل.
Work done by a constant force
اعتبر وجود جسم يتحرك إزاحة مقدارها s تحت تأثير قوة F، وهنا سوف نأخذ حالة بسيطة عندما تكون الزاوية بين متجه القوة ومتجه الإزاحة يساوي صفراً وفي الحالة الثانية عندما تكون هناك زاوية بين متجه الإزاحة ومتجه القوة وذلك للتوصل إلى القانون العام للشغل.
قوة منتظمة في اتجاه الحركة

The work in this case is given by the equation
W = F s
قوة منتظمة تعمل زاوية مع اتجاه الحركة
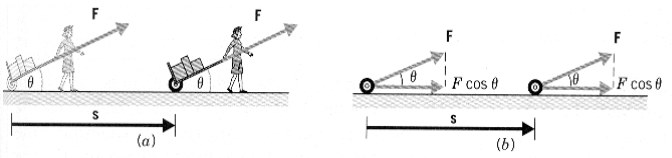
The work in this case is done by the horizontal component of the force
W = F cosq s
The above equation can be written in the directional form as dot product
The unit of the work is N.m which is called Joule (J).
Example
Find the work done by a 45N force in pulling the luggage carrier shown in Figure 4.2 at an angle q = 50o for a distance s = 75m.
Solution
According to equation above the work done on the luggage carrier is
W = (Fcosq ) s = 45 cos 50o × 75 = 2170J
Work can be positive or negative
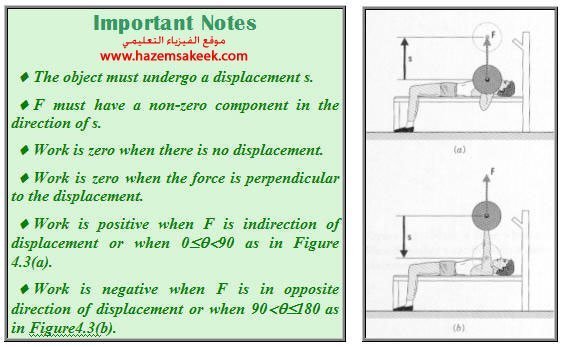
Work done by a varying force
ذكرنا سابقا أن استخدام مفهوم الشغل سوف يساعدنا في التعامل مع الحركة عندما تكون القوة غير منتظمة، ولتوضيح ذلك دعنا نفترض أن قوة منتظمة قدرها 10N تؤثر على جسم ليتحرك مسافة من xi=5m إلى xf=25m وبالتالي فإن الإزاحة مقدارها 20m، ولتمثيل ذلك بيانياً نرسم محور القوة ومحور الإزاحة كما في الشكل، وبالتالي تكون القوة هي خط مستقيم يوازي محور x.

أما في حالة كون القوة متغيرة خلال الإزاحة كما هو مبين في الشكل التالي:

في هذه الحالة نأخذ إزاحة صغيرة قدرها Δx حتى تكون القوة المؤثرة لهذه الإزاحة منتظمة وهنا يكون الشغل المبذول يعطى بالعلاقة التالية:
![]()
وإذا قمنا بتقسيم منحنى القوة إلى أجزاء صغيرة وحسبنا الشغل المبذول خلال كل جزء وجمعناهم، فإنه يمكن التعبير عن ذلك بالعلاقة الرياضية التالية:
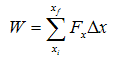 وعند جعل الإزاحة Δx أصغر ما يمكن أي أنها تؤول إلى الصفر لكي نحصل على قيم أدق فإن المعادلة السابقة تتحول إلى
وعند جعل الإزاحة Δx أصغر ما يمكن أي أنها تؤول إلى الصفر لكي نحصل على قيم أدق فإن المعادلة السابقة تتحول إلى
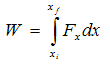
وهذه هي الصورة العامة للشغل (لاحظ أن Fx = F cosq).
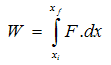
Work done by a spring
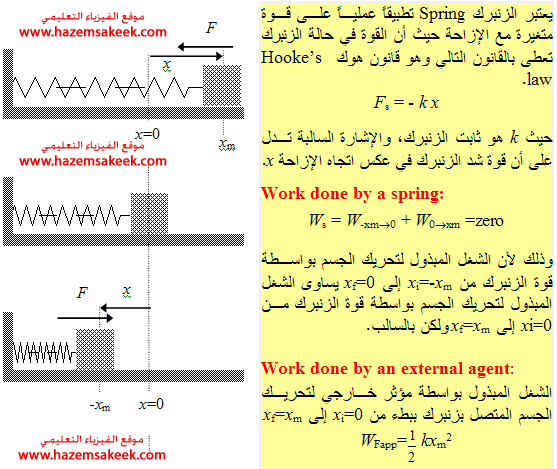
الشكل السابق 4.5 يوضح مراحل إزاحة جسم مرتبط بزنبرك كمثال على القوة المتغيرة حيث أن القوة الاسترجاعية للزنبرك تتغير مع تغير الإزاحة. ولحساب الشغل المبذول بواسطة شخص يشد ببطء الزنبرك من xi=-xm إلى xf=0 نعتبر أن القوة الخارجية Fapp تساوي قوة الزنبرك Fs أي أن
Fapp = – (-kx) = kx
The work done by the external agent is
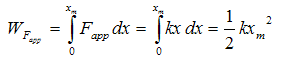
لاحظ أن الشغل المبذول بواسطة قوة خارجية تساوي سالب الشغل المبذول بواسطة قوة شد الزنبرك.
Work and kinetic energy
تعلمنا في أجزاء سابقة أن الجسم يتسارع إذا أثرت عليه قوة خارجية. فإذا فرضنا هنا أن جسم كتلته m يتعرض إلى قوة منتظمة مقدارها F في اتجاه محور x. وبتطبيق قانون نيوتن الثاني نجد أن
Fx = m a
فإذا كانت الإزاحة الكلية التي تحركها الجسم هي s فإن الشغل المبذول في هذه الحالة يعطى بالمعادلة
W = Fx s = (m a) s
ومن معلومات سابقة عن جسم يتحرك تحت تأثير عجلة ثابتة
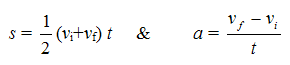
وبالتعويض في معادلة الشغل نحصل على
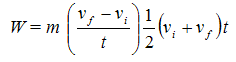
The product of one half the mass and the square of the speed is defined as the kinetic energy of the particle and has a unit of J
K = 1/2 mv2
W = Kf – Ki
This means that the work is the change of the kinetic energy of a particle.
W = ΔK
لاحظ أن طاقة الحركة K دائما موجبة ولكن التغير في طاقة الحركة DK يمكن أن يكون سالباً أو موجباً أو صفراً.
Example
A fighter-jet of mass 5×104kg is travelling at a speed of vi=1.1×104m/s as showing in the Figure. The engine exerts a constant force of 4×105N for a displacement of 2.5×106m. Determine the final speed of the jet.
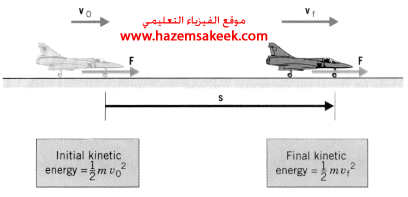
Solution
According to equation of work, the work done on the engine is
W = (Fcosq ) s = 4×105 cos 0o × 2.5×106 = 1×1012J
The work is positive, because the force and displacement are in the same direction as shown in the Figure. Since W = Kf – Ki the final kinetic energy of the fighter jet is
Kf = W + Ki
= (1×1012J) + ½ (5×104kg) (1×104m/s)2 = 4.031×1012J
The final kinetic energy is Kf = ½ mvf2, so the final speed is
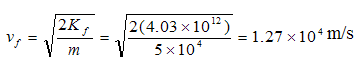
حيث أن المحرك يبذل شغلاً موجباً لذا كانت السرعة النهائية أكبر من السرعة الابتدائية.
Power
The power is defined as the time rate of energy transfer. If an external force is applied to an object, and if the work done by this force is DW it the time interval Dt, then the average power is:
The instantaneous power is given by
The unit of the power is J/s which is called watt (W).
Example
A 65-kg athlete runs a distance of 600 m up a mountain inclined at 20o to the horizontal. He performs this feat in 80s. Assuming that air resistance is negligible, (a) how much work does he perform and (b) what is his power output during the run?
Solution
Assuming the athlete runs at constant speed, we have
WA + Wg = 0
where WA is the work done by the athlete and Wg is the work done by gravity. In this case,
Wg = –mgs(sinq)
So
WA = –Wg = + mgs(sinq)
= (65kg)(9.80m/s2)(600m) sin20o
(b) His power output is given by