محاضرة 6 فيزياء الليزر علاقات اينشتاين The Einstein Relation
علاقات اينشتاين The Einstein Relation
ذكرنا سابقاً أن العلم اينشتين في عام 1917 وضع الاساس النظري لعمل الليزر من خلال دراسة تفاعل الطاقة الكهرومغناطيسية Electromagnetic Radiation مع المادة Matter وذلك من خلال العمليات الإنتقالية الثلاثة التالية:
Absorption process
Spontaneous Emission
Stimulated Emission
افترض اينشتين أن الذرات المكونة للمادة موزعة على مستويين للطاقة هما E0 , E1 حيث أن مستوى الطاقة E0 يعرف باسم Ground State أما مستوى الطاقة E1 فيعرف بـ Excited State. الانتقالات الثلاثة السابقة تحدث في المادة بين مستويي الطاقة عند أي درجة حرارة وهذا ما يعرف بالاتزان الحراري Thermal Equilibrium.
الشكل التالي يوضح مستويي الطاقة وتأثير كل عملية انتقال علي الذرة والاشعاع الكهرومغناطيسي.
 Stimulated Absorption تكون الذرة في المستوى الأول وتنتقل إلى المستوي الثاني بمعدل B12
Stimulated Absorption تكون الذرة في المستوى الأول وتنتقل إلى المستوي الثاني بمعدل B12
Spontaneous Emission تكون الذرة في المستوى الثاني وتنتقل إلى المستوى الأول بمعدل A21
Stimulated Emission تكون الذرة في المستوى الثاني وتنتقل إلى المستوى الأول بمعدل B21
Note: (The terms “excited atoms”, “excited states”, and “excited electrons” are used here with no distinction)
لاحظ أنه عندما يكون انبعاث الفوتونات قليل فإن الانبعاث يكون عشوائي وبزيادة معدل الفوتونات ننتقل إلى حالة الانبعاث الاستحثاثي


| And the atom emits a new photon just like the first one. | A photon strikes an excited atom… |
تعرف المعاملات A21 & B12 & B21 بمعاملات اينشتين Einstein Coefficients وهي التي تعطينا فكرة جيدة عن احتمالية حدوث انتقال بين مستويات الطاقة. وسنقوم بايجاد العلاقات التي تربط هذه المعاملات بعضها ببعض حيث أن الانتقالات الثلاثة تحصل في المادة بصورة مستمرة وبمعدل ثابت لكل منها عند ثبوت درجة الحرارة أي في حالة الاتزن الحراري. وبمعرفة معامل من المعاملات الثلاثة يمكن حساب المعاملات الأخرى.
Population at thermal equilibrium
إن العلاقة بين تعداد الذرات في مستويات الطاقة عند الاتزان الحراري توصف بمعادلة ماكسويل بولتزمان للتوزيع الاحصائي Maxwell-Boltzman Law.
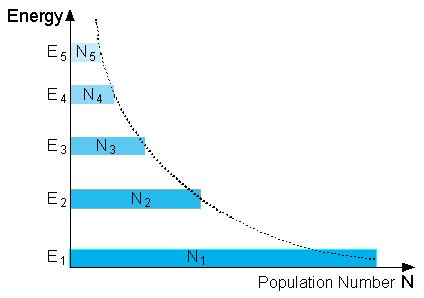
Population Numbers at “Normal Population” |
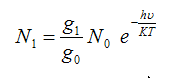
Where T is the temperature in Kelvin and there is a thermal equilibrium at T, g is the statistical weight which represent the different ways of distribution of atoms all have the same energy (degeneracy). |
Example:
Calculate the ratio of the population numbers (N1, N2) for the two energy levels E2and E1 when the material is at room temperature (3000K), and the difference between the energy levels is 0.5 [eV]. What is the wavelength (l) of a photon which will be emitted in the transition from E2 to E1?
Solution:
When substituting the numbers in the equation, we get:
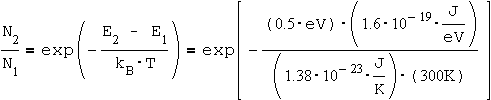
= 4 * 10-9
This means that at room temperature, for every 1,000,000,000 atoms at the ground level (E1), there are 4 atoms in the excited state (E2) !!!
To calculate the wavelength:
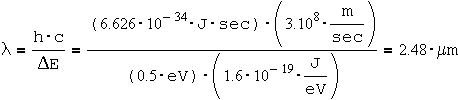
This wavelength is in the Near Infra-Red (NIR) spectrum.
The Rate Equations for the Absorption, Spontaneous Emission and Stimulated Emission
سنقوم في هذه المرحلة بدراسة تأثير كل عملية من العمليات الانتقالية الثلاث على معدل تغير تعداد الذرات N1 في مستوي الطاقة المثار E1 وذلك في حالة الاتزان الحراري dN1/dt، لذا سنفترض مجموعة من الذرات موزعة على مستويين للطاقة E0 , E1
الانبعاث التلقائي Spontaneous Emission
تعتمد عملية الانبعاث التلقائي على تعداد المستوي E1 أي كلما ازداد N1 كلما زادت عملية الانبعاث التلقائي، وكذلك يعتمد هذا الانتقال على المعامل A10 الذي يعبر على احتمالية حدوث الانبعاث التلقائي. يكون معدل التغير في تعداد المستوى E1 بالنسبة للزمن بالسالب لأن كلما زاد معدل التغير كلما نقصت N1. ويمكن التعبير عن ذلك بالمعادلة التالية:
dN1/dt = – A10 N1 (1)
الامتصاص Stimulated Absorption
تعتمد عملية الامتصاص على تعداد المستوي E0 أي كلما ازداد N0 كلما زادت عملية الامتصاص ، وكذلك يعتمد هذا الانتقال على المعامل B01 الذي يعبر على احتمالية حدوث عملية الامتصاص . يكون معدل التغير في تعداد المستوى E1 بالنسبة للزمن بالموجب لأن كلما زاد معدل التغير كلما زاد N1. وحيث أن عملية الامتصاص تحدث اذا توفر Photon ذو طاقة تساوي فرق الطاقة بين المستويين E1 و E0 أي أن
hn = (ΔE) = E2-E1
وللتعبير عن مدى تحقق المعادلة السابقة في عملية الامتصاص فإننا نعبر عنها بكثافة الاشعاع بالدالة ρ كمتغير في التردد Energy density of radiation والتي تعطي مدى احتمالية وجود فوتونات عند تردد ν
ويمكن التعبير تأثير عملية الامتصاص على تغير تعداد المستوى E1 بالمعادلة التالية:
dN1/dt = + B01 N0 ρ(ν) (2)
الانبعاث الاستحثاثي Stimulated Emission
تعتمد عملية الانبعاث الاستحثاثي على تعداد المستوي E1 أي كلما ازداد N1 كلما زادت عملية الانبعاث الاستحثاثي ، وكذلك يعتمد هذا الانتقال على المعامل B10 الذي يعبر على احتمالية حدوث عملية الانبعاث الاستحثاثي. يكون معدل التغير في تعداد المستوى E1 بالنسبة للزمن بالسالب لأن كلما زاد معدل التغير كلما قل N1. وحيث أن عملية الانبعاث الاستحثاثي تحدث اذا توفر Photon ذو طاقة تساوي فرق الطاقة بين المستويين E1 و E0 أي أن
hν = (ΔE) = E2-E1
وللتعبير عن مدى تحقق المعادلة السابقة في عملية الانبعاث الاستحثاثي فإننا نعبر عنها بكثافة الاشعاع بالدالة ρ كمتغير في التردد Energy density of radiation والتي تعطي مدى احتمالية وجود فوتونات عند تردد ν
ويمكن التعبير تأثير عملية الانبعاث الاستحثاثي على تغير تعداد المستوى E1 بالمعادلة التالية:
dN1/dt = – B10 N1 ρ(ν) (3)
المعادلات الثلاثة السابقة الذكر تمثل الحالات المختلفة التي يمكن من خلالها أن تتفاعل الاشعاع الكهرومغناطيسي مع ذرات المادة. وفي حالة الاتزان الحراري عند درجة حرارة T فإن عدد الذرات N1 في مستوى الطاقة E1 يكون ثابت أي أن
N1 = Constant & dN1/dt = zero
Therefore
dN1/dt = – A10 N1 + B01 N0 ρ(ν) – B10 N1 ρ(ν) = 0
Hence
N1 (- A10 – B10 ρ(ν)) + B01 N0 ρ(ν) = 0
N1 ( A10 + B10 ρ(ν)) = B01 N0 ρ(ν)
we get
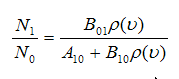 (4)
(4)
وحيث أن المعادلات الثلاثة الأخيرة تم اشتقاقها تحت شرط الاتزان الحراري ولهذا فإن معادلة ماكسويل بولتزمان متحققة
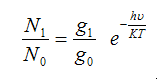 (5)
(5)
وبمقارنة المعادلة (4) بالمعادلة (5) نحصل على المعادلة التالية:
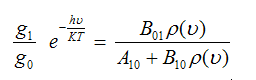 (5*)
(5*)
عند درجات الحرارة العالية فإن كثافة الاشعاع تكون كبيرة وهنا يمكن اهمال تأثير عملية الانبعاث التلقائي حيث انها لا تتأثر بتغير درجة الحرارة.
when KT >> hν we get g1/g0 = N1/N0
hence
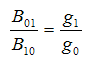 (6)
(6)
From equation (5) we get
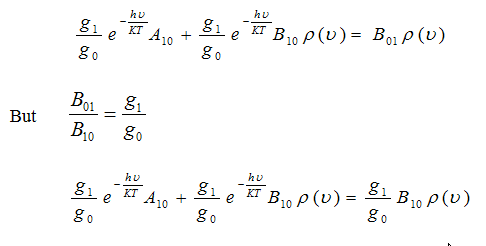
we get
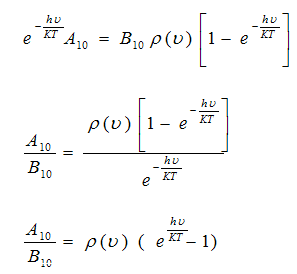
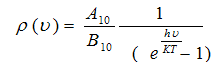 (7)
(7)
Equation (7) called Einstein equation for black body radiation
From the Bank equation of black body radiation
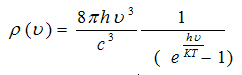 (8)
(8)
we get
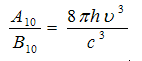 (9)
(9)
The equation (6) and (9) are called Einstein relations. The second relation enables us to evaluate the ratio of the rate of spontaneous emission to the rate of stimulated emission for a given pair of energy levels.
From equation (8)
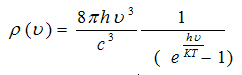
To evaluate the ratio between the spontaneous emission and the stimulated emission
Let R = ![]()
therefore
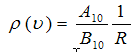
The ratio for the spontaneous emission to the stimulated emission can be written as
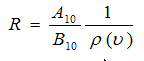
Example
Calculate the ratio of spontaneous emission to stimulated emission for a tungsten filament operating at a temperature of 2000K taking the average frequency to be 5×1014Hz.
Solution
The ratio R = exp[(6.6×10-34*4×1014)/(1.38×10-23*2000)]
تم اهمال كثافة الإشعاع
R = 1.5×105
This confirms that under normal condition of thermal equilibrium stimulated emission is not an important process.
مما سبق نستنتج أن عملية stimulated emission تنافس عمليتي spontaneous emission و absorption وحتى نكبر شعاع ضوئي بواسطة stimulated emission فإنه يجب أن نزيد معدل هذه العملية بالنسبة للعمليتين الاخرتيين. وحتى يتحقق ذلك فإنه يجب زيادة كثافة الاشعاع وتعداد المستوى E1 وهذا مايعرف بـ Population Inversion.


