سنقوم بإدخال مفهوم المجال الكهربي الناشئ عن الشحنة أو الشحنات الكهربية، والمجال الكهربي هو الحيز المحيط بالشحنة الكهربية والذي تظهر فيه تأثير القوى الكهربية. كذلك سندرس تأثير المجال الكهربي على شحنة في حالة أن كون السرعة الابتدائية تساوي صفراً وكذلك في حالة شحنة متحركة.
في هذا المحاضرة سنقوم بإدخال مفهوم المجال الكهربي الناشئ عن الشحنة أو الشحنات الكهربية، والمجال الكهربي هو الحيز المحيط بالشحنة الكهربية والذي تظهر فيه تأثير القوى الكهربية. كذلك سندرس تأثير المجال الكهربي على شحنة في حالة أن كون السرعة الابتدائية تساوي صفراً وكذلك في حالة شحنة متحركة.
3.1 The Electric Field
The gravitational field g at a point in space was defined to be equal to the gravitational force F acting on a test mass mo divided by the test mass
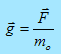 (3.1)
(3.1)
In the same manner, an electric field at a point in space can be defined in term of electric force acting on a test charge qo placed at that point.
3.2 Definition of the electric field
The electric field vector E at a point in space is defined as the electric force F acting on a positive test charge placed at that point divided by the magnitude of the test charge qo
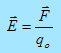 (3.2)
(3.2)
The electric field has a unit of N/C
لاحظ هنا أن المجال الكهربي E هو مجال خارجي وليس المجال الناشئ من الشحنة qo كما هو موضح في الشكل 3.1، وقد يكون هناك مجال كهربي عند أية نقطة في الفراغ بوجود أو عدم وجود الشحنة qo ولكن وضع الشحنة qo عند أية نقطة في الفراغ هو وسيلة لحساب المجال الكهربي من خلال القوى الكهربية المؤثرة عليها.

Figure 3.1
3.3 The direction of E
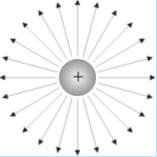
If Q is +ve the electric field at point p in space is radially outward from Q as shown in figure 3.2(a).
If Q is -ve the electric field at point p in space is radially inward toward Q as shown in figure 3.2(b).
 Figure 3.2 (a) Figure 3.2 (b)
Figure 3.2 (a) Figure 3.2 (b)
يكون اتجاه المجال عند نقطة ما لشحنة موجبة في اتجاه الخروج من النقطة كما في الشكل 3.2(a)، ويكون اتجاه المجال عند نقطة ما لشحنة سالبة في اتجاه الدخول من النقطة إلى الشحنة كما في الشكل 3.2(b).
3.4 Calculating E due to a charged particle
Consider Fig. 3.2(a) above, the magnitude of force acting on qo is given by Coulomb’s law
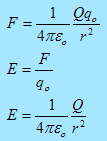 (3.3)
(3.3)
3.5 To find E for a group of point charge
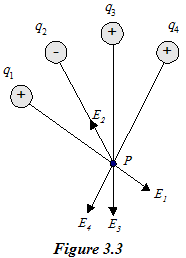 To find the magnitude and direction of the electric field due to several charged particles as shown in figure 3.3 use the following steps
To find the magnitude and direction of the electric field due to several charged particles as shown in figure 3.3 use the following steps
(1) نرقم الشحنات المراد إيجاد المجال الكهربي لها.
(2) نحدد اتجاه المجال الكهربي لكل شحنة على حده عند النقطة المراد إيجاد محصلة المجال عندها ولتكن النقطة p، يكون اتجاه المجال خارجاً من النقطة p إذا كانت الشحنة موجبة ويكون اتجاه المجال داخلاً إلى النقطة إذا كانت الشحنة سالبة كما هو الحال في الشحنة رقم (2).
(3) يكون المجال الكهربي الكلي هو الجمع الاتجاهي لمتجهات المجال
Ep = E1 + E2 + E3 +E4 …………. (3.4)
(4) إذا كان لا يجمع متجهات المجال خط عمل واحد نحلل كل متجه إلى مركبتين في اتجاه محوري x و y
(5) نجمع مركبات المحور x على حده ومركبات المحور y.
Ex = E1x + E2x + E3x +E4x
Ey = E1y + E2y + E3y +E4y
(6) تكون قيمة المجال الكهربي عند النقطة الفراغ هي ![]()
(7) يكون اتجاه المجال هو ![]()
3.6 Electric field lines
The electric lines are a convenient way to visualize the electric filed patterns. The relation between the electric field lines and the electric field vector is this:
(1) The tangent to a line of force at any point gives the direction of E at that point.
(2) The lines of force are drawn so that the number of lines per unit cross-sectional area is proportional to the magnitude of E.
Some examples of electric line of force
 |
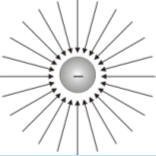 |
| Electric field lines due to +ve charge | Electric field lines due to -ve charge |
 |
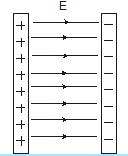 |
| Electric field lines due to +ve line charge | Electric field lines due two surface charge |
Figure 3.7 shows some examples of electric line of force
Notice that the rule of drawing the line of force:-
(1) The lines must begin on positive charges and terminates on negative charges.
(2) The number of lines drawn is proportional to the magnitude of the charge.
(3) No two electric field lines can cross.
3.7 Motion of charge particles in a uniform electric field
If we are given a field E, what forces will act on a charge placed in it?
We start with special case of a point charge in uniform electric field E. The electric field will exert a force on a charged particle is given by
F = qE
The force will produce acceleration
a = F/m
where m is the mass of the particle. Then we can write
F = qE = ma
The acceleration of the particle is therefore given by
a = qE/m (3.7)
If the charge is positive, the acceleration will be in the direction of the electric field. If the charge is negative, the acceleration will be in the direction opposite the electric field.
One of the practical applications of this subject is a device called the (Oscilloscope) See appendix A (Cathode Ray Oscilloscope) for further information.
والأمثلة توضح تطبيقاً على ما سبق ذكره. انتقل إلى التمارين الاضافية لدراسة الامثلة………..
3.9 The electric dipole in electric field
If an electric dipole placed in an external electric field E as shown in figure 3.14, then a torque will act to align it with the direction of the field.
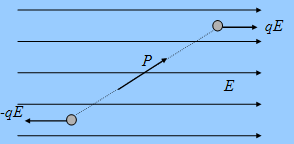
Figure 3.14
t = P E sin q (3.11)
where P is the electric dipole momentum, q the angle between P and E
يكون ثنائي القطب في حالة اتزان equilibrium عندما يكون الازدواج مساويا للصفر وهذا يتحقق عندما تكون (θ= 0 , π)

Figure 3.15(ii) Figure 3.15 (i)
في الوضع الموضح في الشكل i3.15 عندما θ=0 يقال إن الـ dipole في وضع اتزان مستقر stable equilibrium لأنه إذا أزيح بزاوية صغيرة فانه سيرجع إلى الوضع θ=0، بينما في الوضع الموضح في الشكلii3.15 يقال إن الـ dipole في وضع اتزان غير مستقر unstable equilibrium لأن إزاحة صغيرة له سوف تعمل على أن يدور الـ dipole ويرجع إلى الوضع θ=0 وليس θ=π.
والأمثلة توضح تطبيقاً على ما سبق ذكره. انتقل إلى التمارين الاضافية لدراسة الامثلة……….


