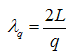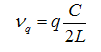علمنا من المحاضرات السابقة أنه للحصول على الليزر نستخدم التغذية العكسية بواسطة المرايا وذلك لتكبير الشعاع الضوئي خلال مروره بالوسط المشع لليزر، لهذه المرايا دور في التأثير على الاشعاع الكهرومغناطيسي داخل المكبر حيث ينتج نوعين من الانماط تعرف بالانماط الطولية longitudinal modes والنماط المستعرضة transverse modes.
Longitudinal modes only specific frequencies are possible inside the optical cavity of a laser, according to standing wave condition.
Transverse modes are created in cross section of the beam, perpendicular to the optical axis of the laser.
Longitudinal modes (Axial Modes)
Using Fabry-Perot interferometer one can observe that the output of the laser beam consists of a number of discrete frequency components. These modes are known as longitudinal modes or axial modes. These modes are created inside the optical resonator between the two mirrors.
إن السبب يعود في تكون هذه الانماط يعود إلى تكون أمواج موقوفة standing wave بين المرآتين. وكما نعلم أن الأمواج الموقوفة تتكون نتيجة لتداخل موجتين لهما نفس التردد وتنتشران في اتجاهين متعاكسين في المسافة بين المرآتين. وكمثال على هذه الأمواج الوتر الموسيقي في الجيتار.
Standing waves in a laser
In a laser an optical cavity is created by two mirrors at both ends of the laser.
These mirrors serve two goals:
-
They increase the length of the active medium, by making the beam pass through it many times.
-
They determine the boundary conditions for the electromagnetic fields inside the laser cavity.
The axis connecting the centers of these mirrors and perpendicular to them is called Optical Axis of the laser. The laser beam is ejected out of the laser in the direction of the optical axis.
An electromagnetic wave which move inside the laser cavity from right to left, is reflected by the left mirror, and move to the right until it is reflected from the right mirror, and so on.
Thus, two waves of the same frequency and amplitude are moving in opposite directions, which is the condition for creating a standing wave.
Conditions for Standing Waves
standing waves, must fulfill the condition:
L = q λq/2
L = Length of the optical cavity.
q = Number of the mode, which is equal to the number of half wavelengths inside the optical cavity. The first mode contains half a wavelength, the second mode 2 halves (one) wavelength.
λq = Wavelength of mode m inside the laser cavity.
In fact the number of modes (q) in most laser is very large. For Example if the central wavelength is 500nm and the mirror separation is 25cm , q has a value of 1000000, since q can be any integer, there are many possible wavelengths within the laser transition shape.
Example
The length of an optical cavity is 25 [cm]. Calculate the frequencies nmand wavelengths lm of the following modes:
-
m =1
-
m = 10
-
m = 100
-
m = 106
Solution
|
|
|
|
|
1
|
|
n1 = 6*108 [Hz]
Radio Wave
|
|
2
|
|
n2 = 6*109 [Hz]
Short Wave Communication
|
|
3
|
|
n3 = 6*1010 [Hz]
Microwaves
|
| 4 | 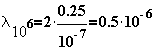 |
n4 = 6*1014 [Hz]
Green Color
|
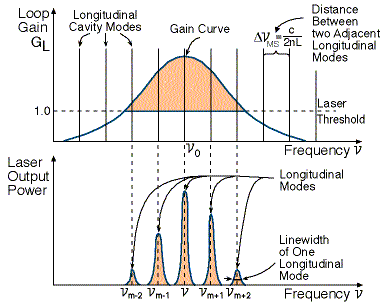
The separation between axial modes
If the First mode is q
Then
L = q λq / 2
If the Second mode is q+1
Then
L = (q+1) λq+1 / 2
It is more convenient to refer to the axial modes by their frequency
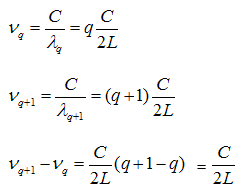
The separation between neighboring frequencies is equal to C/2L i.e.dependent only on the separation between mirrors and independent of q.
For L = 25cm The separation between neighboring frequencies is 6×108sec-1.
ملاحظات
![]() تزداد عدد الأنماط تحت منحنى الحصيلة كلما زاد طول مكبر الليزر Lوذلك لأن الفاصل بين الأنماط يقل بزيادة L.
تزداد عدد الأنماط تحت منحنى الحصيلة كلما زاد طول مكبر الليزر Lوذلك لأن الفاصل بين الأنماط يقل بزيادة L.
It is clear that a single mode laser can be made by reducing the length of the cavity, such that only one longitudinal mode will remain under the fluorescence curve with GL>1.
عدد الأنماط التي يمكن أن تنتج ليزر تلك التي يتحقق عندها شرط الحصيلة أكبر من او يساوي الخسارة كما هو واضح في المنطقة الملونة في الشكل أعلاه.
للحصول على عدد الأنماط التي يمكن أن تكبر تحت منحنى الحصيلة نقسم Laser bandwidth على المسافة بين نمطين C/2L.
The approximate number of possible laser modes is given by the width of the Laser bandwidth divided by the distance between adjacent modes:
Example
The length of the optical cavity in He-Ne laser is 30 [cm]. The emitted wavelength is 0.6328 [mm]. Calculate:
1. The difference in frequency between adjacent longitudinal modes.
2. The number of the emitted longitudinal mode at this wavelength.
3. The laser frequency.
Solution
1. The equation for difference in frequency is the same as for the basic mode:
(Delta ν) = C/(2L) = 3*108 [m/s]/(2*0.3 [m]) = 0.5*109[Hz] = 0.5 [GHz]
2. From the equation for the wavelength of the qth mode:
λq = 2L/m
q = 2L/ λq = 2*0.3 [m]/0.6328*10-6 [m ] = 0.948*106
which means that the laser operate at a frequency which is almost a million times the basic frequency of the cavity.
3. The laser frequency can be calculated in two ways:
a) By multiplying the mode number from section 2 by the basic mode frequency:
ν = q*(Delta ν) = (0.948*106)(0.5*109 [Hz]) = 4.74*1014 [Hz]
b) By direct calculation:
ν = c/λ = 3*108 [m/s]/0.6328*10-6 [m ] = 4.74*1014 [Hz]
Example
The length of the optical cavity in He-Ne laser is 55 [cm]. The Laser bandwidth is 1.5 [GHz]. Find the approximate number of longitudinal laser modes.
Solution
The distance between adjacent longitudinal modes is:
Δν = c/(2L) = 3*108 [m/s]/(2*0.55 [m]) = 2.73*108 [m/s] = 0.273 [GHz]
The approximate number of longitudinal laser modes:
N =Laser bandwidth /Δν = 1.5 [GHz]/0.273 [GHz] = 5.5 » 5
The importance of Longitudinal Optical Modes at the Output of the Laser
The importance of Longitudinal modes of the laser is determined by the specific application of the laser.
-
In most high power applications for material processing or medical surgery, the laser is used as a mean for transferring the energy to the target. Thus there is no importance for the longitudinal laser modes.
-
In applications where interference of electromagnetic radiation is important, such as holography or interferometric measurements, the longitudinal modes are very important.
-
In spectroscopic and photochemical applications, a very defined wavelength is required. This wavelength is achieved by operating the laser in single mode, and than controlling the length of the cavity , such that this mode will operate at exactly the required wavelength. The structure of longitudinal laser modes is critical for these applications.
-
When high power short pulses are needed, mode locking is used. This process causes constructive interference between all the modes inside the laser cavity. The structure of longitudinal laser modes is important for these applications.
Transverse modes
بدراسة توزيع شدة اشعة الليزر على مساحة المقطع عمودياً على المحور الضوئي لليزر Optical axis laser وجد أنها تأخذ أشكال مختلفة تعتمد على دقة موقع المرايا وأي تغير طفيف يؤدي إلى تغيير هذه الاشكال والتي تعرف بالأنماط المستعرضة Transversal Mode.
باسقاط شعاع ليزر على شاشة بيضاء بعد تكبيره بواسطة عدسة مفرقة يمكن فحص الانماط المستعرضة لشعاع الليزر. والشكل التالي يوضح مجموعة من هذه الأشكال حيث يبين اللون الأخضر اكبر شدة لليزر والمناطق البيضاء ينعدم فيها الليزر.
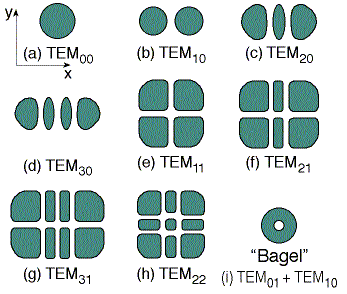
Transverse distribution of intensity
A small misalignment of the laser mirrors causes different path length for different “rays” inside the cavity. Thus, the distribution of intensity is not the perfect gaussian distribution.
Each transverse mode (TEM) is marked with two indexes: TEMmn m, n, are integer numbers. Assuming the beam advance in z direction:
m = Number of points of zero illumination (between illuminated regions) along x axis.
n = Number of points of zero illumination (between illuminated regions) along y axis.