محاضرة 9 مغناطيسية وتيار متردد

تابع الحث الذاتي والحث المتبادل Inductance: تذبذبات دائرة الملف والمكثف Oscillations in an LC circuit

عند توصيل مكثف مشحون بملف حلزوني كما في الشكل فإن التيار يتذبذب بين المكثف والملف إلى مالانهاية اذا افترضنا ان مقاومة الدائرة تساوي صفر.  لندرس بالتفصيل ماذا يحدث عند اغلاق المفتاح S في الدائرة على شكل خطوات متسلسلة:

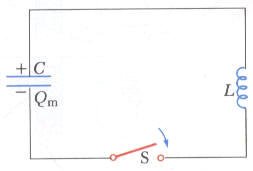
1. في البداية تكون الشحنة الكلية على المكثف اكبر ما يمكن وتساوي Q_m.  وهذا يعني ان طاقة مخزنة في المكثف وتعطى بالمعادلة U=Q_m²/2C.  في حين أن الملف لا يختزن طاقة.
2. عند اغلاق المفتاح S يبدأ المكثف في تفريغ شحنته وتنتقل الشحنة في صورة تيار كهربي إلى الملف الحلزوني وبهذا تقل الطاقة المختزنة في المكثف (في صورة مجال كهربي) وتزداد الطاقة المخزنة في الملف الحلزوني (في صورة مجال مغناطيسي).
3. يستمر انتقال الطاقة من المكثف إلى الملف إلى أن يفقد المكثف شحنته وتصبح الطاقة بالكامل مخزنة في الملف الحلزوني.
4. تتكرر العملية السابقة ولكن في الاتجاه المعاكس وتستمر حتي تنتقل الطاقة من الملف إلى المكثف وهكذا….

تناظر هذه العملية حركة الكتلة المثبتة بزنبرك على سطح افقي عديم الاحتكاك

باستخدام مبدأ الحفاظ على الطاقة يمكن دراسة هذه الظاهرة عند أي زمن t وايجاد علاقة بين شحنة المكثف والتيار في الملف.  علما بأن الطاقة الابتدائية هي U وهذه الطاقة تبقى ثابتة (المقاومة مهملة) ولكن تتوزع على صورة طاقة حركة و طاقة وضع.

   *

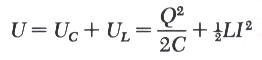وباجراء عملة التفاضل بالنسبة للزمن مع الاخذ بعين الاعتبار ان الطاقة الكلية ثابتة لأننا اهملنا المقاومة نحصل على مايلي

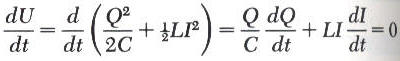
بالتعويض عن التيار في المعادلة I=dQ/dt وذلك لتبسيط المعادلة وجعلها في متغير واحد فقط

        **

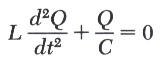
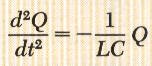وهذه معادلة تفاضلية متجانسة من الدرجة الثانية وهي نفس صورة معادلة الحركة التوافقية البسيطة للكتلة المثبتة في زنبرك حيث أن التغير في الازاحة بالنسبة للزمن يعطى بالعلاقة التالية:

حيث k ثابت الزنبرك و m الكتلة المثبتة في الزنبرك وω التردد الزاوي

^ω2 = k/m

ومعادلة الحركة التوافقية البسيطة لها حل من الصورة

ω is the angular frequency

A is the amplitude of the motion (maximum displacement)

d is the initial phase (the position at time t=0)

وباستخدام ما سبق للحركة التوافقية البسيطة للكتلة والزنبرك نطبق على حالة شحنة المكثف والتي تتذبذب مع الزمن خلال انتقال الطاقة بين المكثف والملف في صورة حركة توافقية بسيطة.

المعادلة ** لها حل يعطى بالمعادلة التالية:

Q_m is the maximum charge on the capacitor and the angular frequency ω is given by

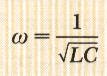
وهذا يشير إلى أن التردد الزاوي يعتمد على كلا من سعة المكثف والحث الذاتي للملف الحلزوني.

ماذا عن التيار المار في الدائرة؟

حيث أن العلاقة بين التيار الكهربي المار في الدائرة والشحنة هي I=dQ/dt سنقوم باجراء التفاضل بالنسبة للزمن لإيجاد علاقة التيار الكهربي المار في الدائرة مع الزمن والناتج من انتقال الطاقة بين المكثف والملف.

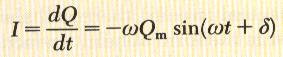
عند زمن t=0 فإن التيار يساوي صفر ويمكن اثبات ان الطور الابتدائي Initial phase δ يساوي صفر ايضاً.

وعليه يمكن التعبير عن التغير في كلاً من الشحنة والتيار مع الزمن من خلال المعادلتين التاليتين:

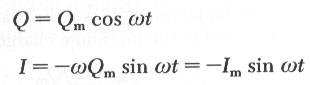
where  I_m = ω Q_m

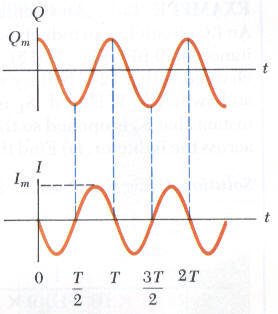
يبين الشكل المقابل علاقة الشحنة Q مع الزمن t وعلاقة التيار I مع الزمن t.  لاحظ أن الشحنة تتذبذب بين القيمة Q_m والقيمة في الاتجاه السالب Q_m والتيار يتذبذب بين القيمة I_m والقيمة I_m في الاتجاه السالب، ولكن التيار يختلف في الطور مع الشحنة بزاوية قدرها 90 درجة.  أي أن عندما تكون الشحنة قيمة عظمى يكون التيار صفراً وعندما تكون الشحنة صفراً يكون التيار قيمة عظمى.

ماذا عن الطاقة الكلية؟

بالتعويض عن كلا من الشحة والتيار في المعادلة * نحصل على المعادلة التالية:

***

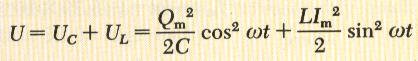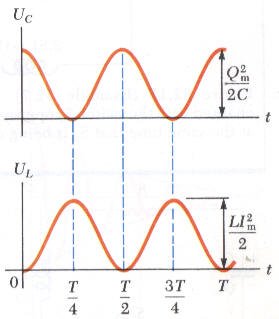
تصف معادلة الطاقة الكلية ماذا يحدث للشحنة والتيار كدالة في الزمن وهو ما تم وصفه في الخطوات الأربعة في بداية المحاضرة. وبالرسم البياني لعلاقة كلاً من الطاقة المختزنة في المكثف والطاقة المختزنة في الملف مع الزمن نستنتج أن عندما تكون الطاقة المختزنة في المكثف أكبر ما يمكن تكون قيمة الطاقة المختزنة في الملف تساوي صفر والعكس صحيح. ولكن عند أي زمن t فإن الطاقة الكية تبقى ثابتة وتساوي مجموع الطاقتين.  وحيث أنه عند القيمة العظمي للشحنة والقيمة العظمي للتيار تكون الطاقتين متساويتين وهذا يمكن التعبير عنه من خلال المعادلة التالية:

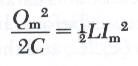
بالتعويض في المعادلة *** نحصل على المعادلة التالية:

U = Q_m²/2C

وهذا متحقق فقط في حالة اهمال المقاومة أي لا يوجد فقد في الطاقة على صورة طاقة حرارية.