ظاهرة دوبلر من الظواهر الفيزيائية المعروفة والتي نلاحظها في حياتنا العملية حينما تمر سيارة إسعاف أو سيارة الإطفاء مسرعة وبينما يصدر عنها صوت الإنذار فإننا نسمع ترددات مختلفة بينما تكون السيارة مقتربة منا او مبتعدة عنا وهذا الصوت يختلف تردده عن التردد الذي يسمعه سائق السيارة لأنه يكون ثابت بالنسبة للصوت، ومن هذا يمكن تعريف ظاهرة دوبلر على إنها إزاحة للتردد نتيجة للحركة النسبية بين المصدر والمراقب. فعندما يكون المصدر مقترب من المراقب يكون التردد المقاس أعلى من التردد الأصلي أي مزاح ناحية الترددات الأعلى بينما يكون التردد اقل من التردد المقاس أي مزاح ناحية الترددات الأقل إذا كان المصدر مبتعدا عن المراقب. وظاهرة دوبلر تعتمد على السرعة النسبية بين المصدر والمراقب.
إذا كنا نتعامل مع تردد الأمواج الصوتية الصادرة عن حركة سيارة او طائرة حيث تكون السرعات اقل بكثير من سرعة الضوء فإننا نتحدث عن ظاهرة دوبلر الكلاسيكية أما إذا كنا نتعامل مع الأمواج الكهرومغناطيسية التي تنتشر بسرعة الضوء فإننا نتحدث عن ظاهرة دوبلر النسبية..
لفهم المقصود بظاهرة دوبلر استعن بالتجربة الموضحة في النموذج ولاحظ ما يحدث للأمواج الصوتية مع اختلاف السرعة النسبية بين المصدر والراصد.
يستخدم شرطة المرور ظاهرة دوبلر في تقدير سرعة السيارات على الطريق من مقارنة الترددات الصوتية الصادرة عن محرك السيارة بمقارنة الترددات للسيارة الثابتة والسيارة المتحركة ومن ثم حساب قيمة السرعة للسيارة. كذلك يستخدم الفلكيون ظاهرة دوبلر في قياس سرعة النجوم والمجرات بالنسبة للأرض وإذا كانت مقتربة منا أو مبتعدة عنا من خلال قياس تردد الأشعة الكهرومغناطيسية الصادرة عن النجوم ومقارنتها بتلك الترددات الصادرة عندما تكون في المختبر أي ثابتة بالنسبة للمراقب.
ظاهرة دوبلر الكلاسيكية
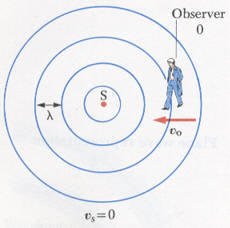
الحالة الأولى عندما يكون المراقب متحرك والمصدر الصوتي ثابت
The frequency of the source is f and the wavelength is λ and the velocity of sound is v..
When vs = 0 & vo = 0 the observed frequency = the source frequency.
When the observer moves towards the source, the speed of the waves relative to the observer is v’=v+vo but l does not change. Hence the frequency heard by the observer is increased and given by.
f’ = v’/λ = v+vo/λ since λ=v/f
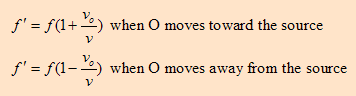
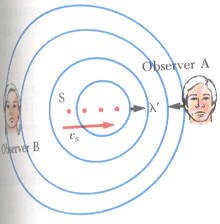
الحالة الثانية عندما يكون المراقب ثابت والمصدر الصوتي متحرك
If the source moves toward the observer OA, the wave fronts seen by the observer are closer together as a result of the motion of the source in the direction of the outgoing wave. As a result the wavelength l’ measured by OA is shorter than the wavelength l of the source.
لاحظ ان كل اهتزازة تستغرق زمن دوري T وخلال هذا الزمن الدوري بكون المصدر قد تحرك مسافة تساوي vsT او vs/f وعليه يتغير الطول الموجي بمقدار Δλ
Δλ = vs/f
وعليه يكون الطول الموجي المعدل ‘l يعطى بالعلاقة التالية
λ’ = λ – Δλ = λ – (vs/f)
وعليه يكون التردد المسموع بواسطة المراقب OA هو التردد ‘f
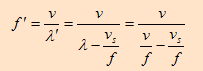

وهذا يعني ان التردد المسموع اكبر من تردد المصدر ‘f < f

وهذا يعني ان التردد المسموع اكبر من تردد المصدر ‘f > f
ظاهرة دوبلر النسبية
في حالة التعامل مع سرعات قريبة من سرعة الضوء فإن ظاهرة دوبلر الكلاسيكية لا تأخذ في الحسبان فرضيات النظرية النسبية في ان سرعة الضوء ثابتة بالنسبة لجميع محاور الاسناد. ولهذا سنقوم من خلال المثال التالي باشتقاق معادلات التغير في التردد في حالة السرعات الكبيرة المقارنة.
مثال توضيحي
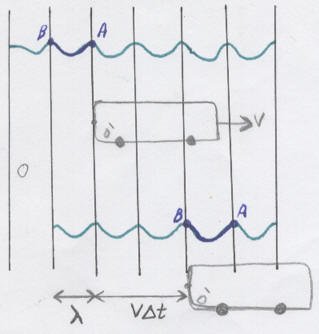
افترض أن عربة متحركة بسرعة v بالنسبة لمراقب O وكانت هناك موجة ضوئية تنتشر في نفس اتجاه حركة العربة كما في الشكل المقابل
الحدث الاول: وصول جبهة الموجة A إلى مؤخرة العربة.
الحدث الثاني: وصول جبهة الموجة الذي يعقبه B إلى مؤخرة العربة أيضا.
نلاحظ هنا ان المراقب ‘O هو المراقب الثابت بالنسبة للحدثين بينما المراقب O متحرك بالنسبة للحدثين.
For O c = λ f
For O’ c = λ’ f’
Where λ is the wavelength and n is the frequency. Note that the time measurements are exists f&f’ in and the space measurements are exists in λ&λ’
| With respect to O | ‘With respect to O |
| Δx = vΔt | Δx’ = 0 |
where Δt is the time interval between the two events with respect to O, however the time interval between the two events with respect to O’ is Δt’.
Since the wave AB moves only one wavelength λ’ then the time required is 1/f’
Δt’ = 1/f’
سنقوم بحساب الفارق الزمني Δt بالنسبة للمراقب O
حيث أن المسافة التي انتقلتها الموجة AB بالنسبة للمراقب O هي كما هو موضح في الشكل أعلاه هي vΔt+λ
وتكون سرعة الموجة AB
c = (vΔt+λ) / Δt
therefore,
Δt (c-v) = λ = c/f
Δt (1-v/c) = 1/f
| With respect to O | With respect to O’ |
|
Δt = 1/f(1-β) |
Δt’ = 1/f’ |
لاحظ هنا ان العلاقة بين القياسات الزمنية للمراقب O والمراقب ‘O هي علاقة تأخير زمني لان المراقب O سيقيس زمن اكبر من زمن المراقب ‘O لأنه متحرك بالنسبة للحدث.
![]()
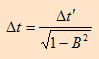
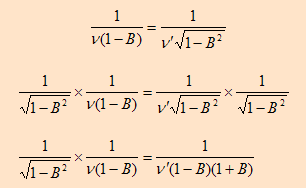
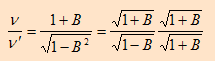
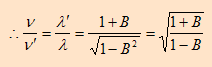
when v and c are in the same direction then f>f’
وهذا يتحقق عندما يكون المصدر مقترباً من المراقب
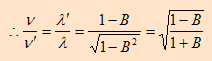
when v and c are in the opposite direction then f<f’
وهذا يتحقق عندما يكون المصدر مبتعداً عن المراقب
تجربة عملية للتوضيح
عند قياس التردد الأصلي للمبة الصوديوم في المختبر (اللمبة التي تستخدم لإنارة الطرق في الليل والتي يكون الضوء المنبعث عنها بين الأصفر والبرتقالي). فإذا ما ثبتت اللمبة على مركبة فضائية مبتعدة عنا بسرعة قريبة من سرعة الضوء فإن ترددها المقاس سوف يكون اصغر من التردد الأصلي ويكون لون الضوء المنبعث في هذه الحالة قريبا من اللون الأحمر. أما إذا كانت المركبة الفضائية مقتربة منا فإن الضوء المنبعث عنها يكون ذو لون ازرق وهذا يعود إلى ان التردد المعدل اكبر من التردد الأصلي.
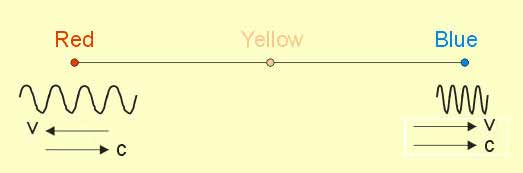
إذا كان المصدر مقترباً منا فإن التردد المقاس يكون اكبر من التردد الأصلي ويحدث ما يسمي بالانزياح ناحية الأزرق Blue Shift أي يزاح اللون ناحية الترددات الأعلى.
وإذا كان المصدر مبتعد عنا فإن التردد المقاس يكون اقل من التردد الأصلي ويحدث ما يسمى بالانزياح ناحية الأحمر Red Shift أي يزاح اللون ناحية الترددات الأقل.
وهذا ما يحدث في الطبيعة حيث يوجد نجوم الكويزار Quasar وهو نجم بعيد جداً يبتعد عنا بسرعة كبيرة فإذا ما كان الضوء المنبعث من النجم ناتج عن احتراق غاز الهيدروجين ومن المعروف أن الطول الموجي لطيف الهيدروجين مقاس في المختبر بدقة. فإذا ما قورن بالطول الموجي القادم من نجم الكويزار والمقاس بواسطة التلسكوبات الأرضية فقد وجد أن التردد المقاس إلى التردد الأصلي في المختبر كالنسبة
![]()
وهذا يعني أن التردد المقاس اصغر من التردد الأصلي أي ان النجم مبتعد عنا وأن سرعة النجم في عكس سرعة الضوء القادم لنا لذا نستخدم المعادلة التالية:
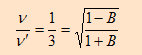
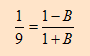
B = 8/10
v = 0.8c
أي أن نجم الكويزار يبتعد عنا بسرعة تصل إلى 80% من سرعة الضوء.







مع كامل تقديري للجهود المبذولة، إلا أن هناك خطأبسيط في هذه المحاضرة يجب التنويه عليه فقط بغرض التوضيح لطلابنا العرب الزائرين بغيةالاستفادة من هذا الموقع الرائع.
الغلط هو في التردد الصادر f والتردد المسموع fً وذلك تحديدا في علاقة التردد المسموع والصادر الحالة الثانية من ظاهرة دوبلر الكلاسيكية حيث يجب أن يكون في الحالة الأولى التردد المسموع أكبر من الصادر وفي حالة ابتعاد المصدر عن المراقب يجب أن يكون الصادر أكبر من المسموع.
ودمتم بالف خير