معادلة ديراك
أ. محمد ماهر عبد الرحيم محمد
بعد انطلاق شرارة ثورة ميكانيكا الكم في بداية القرن الماضي، هرع الفيزيائيون في تلك الفترة الى محاولة السيطرة على هذه النظرية الغريبة – والتى تناقض العقل الكلاسيكي بصورة واضحة – بواسطة احكام الصياغة الرياضية والتي يجب ان تصف الواقع الكمي وتتفق مع التجارب ولو كان ذلك على حساب مبدأ السببية او الحتمية. فمع ظهور الميكانيك الكمي انهدم صرح الحتمية فعند القيام بالتجربة تحت نفس الشروط مرتين متتابعتين نحصل على نتائج مختلفة، بغض النظر عن الجدال الفلسفي حول هذا الموضوع وعلى طريقة” بول ديراك” – الذي كان يهتم بالمعادلات اكثر من الجدال والكلام – في احدى المحاضرات وقف الفيزيائي النمساوي “اروين شرودنجر” يلقي محاضرته حول مفهوم الدالة الموجية، و الذي ظهر اول مرة مع الفيزيائي “ماكس بورن”، وفجأة في اثناء محاضرة شرودنجر الاسطورية والتى كانت تبدو مملة في نظر احدهم فوجه سؤال الى السيد “شرودنجر” قائلا: يا سيد لقد صدعت رؤوسنا بدالتك الموجية، فاين هي معادلة الموجة؟ فكان سؤاله هو ما دفع “شرودنجر” الى صياغة معادلته المشهورة والتى لعبت دورا محوريا في صياغة النسخة الموجية في ميكانيكا الكم، فكانت معادلة تفاضلية يمثل حلها دالة الموجة للنظام الكمي المراد دراسته.
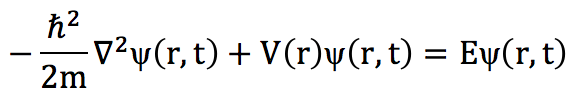
كانت اولى المحاولات لايجاد نسخة نسبية من هذه المعادلة هي ما يعرف بمعادلة “كلين-جوردون ” والمقصود بالنسخة النسبية ان نضع في الاعتبار مبادئ النسبية الخاصة واهمها عدم الفصل بين الزمان والمكان، فعند النظر في معادلة شرودنجر السابقة نجد ان المشتقة المكانية من الرتبة الثانية {∇2 ψ(r,t)} بينما المشتقة الزمانية من الرتبة الاولى {Eψ(r,t)=iℏ ∂/∂t ψ(r,t)}، فكانت الخطوة الاولى نحو اشتقاق نسخة نسبوية من معادلة شرودنجر هي مساواة رتب المشتقات، وتجسدت محاولة كلين وجوردون في جعل كل من المشتقتين الزمانية والمكانية من الرتبة الثانية بعد التعويض بقيم المؤثرات الكمية للطاقة وكمية الحركة في معادلة الطاقة النسبية (E2=P2+m2) باعتبار (ℏ=c=1) وكانت النتيجة:
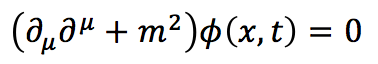
وهي ما يعرف بمعادلة (كلين-جوردون)، ولكن سرعان ما ظهرت المشاكل ، فبمجرد جعل المشتقة الزمانية من الرتبة الثانية ادى ذلك الى ظهور قيم احتمالية سالبة (كثافة الاحتمال سالبة!!!! …..غريب و غير منطقي)، وكانت المشكلة الثانية متمثلة في حل هذه المعادلة حيث من الواضح ان الحل يجب ان يمثل طاقة الجسيمات ولكن المفاجأة كانت في ان هذه الطاقة تمتلك قيمتين سالبة وموجبة.
بمجرد ظهور هذه المشاكل عجزت المعادلة عن تخطيها مما دفع الفيزيائي الرياضي “بول ادريان ديراك” ان يبحث في اصل المشكلة، ففطن ديراك بعقله الرياضي المدرب الى ان المشكلة تكمن في رتبة المعادلة –بخصوص الاحتمالية- و في التفسير-بخصوص الطاقة السالبة. لذلك عكف على محاولة الحصول على معادلة نسبية تفاضلية تكون من الرتبة الاولى بخصوص المشتقات الزمانية والمكانية، بدون الخوض في التحليلات التى اتبعها بالرغم من سهولتها ولكنها تأخذ مساحة لا يمكن توفيرها في هذه المقال، في النهاية حصل السيد ديراك على معادلته المشهور:
![]()
بهذه الطريقة نجح ديراك في التخلص من مشكلة الاحتمالية السالبة، من جانب اخر حصل على نفس الحلول السالبة للطاقة ولكنه كما قال فان المشكلة هنا مشكلة تفسير، لذلك اقترح امكانية وجود جسيمات مضادة تحمل طاقة موجبة تتشابه مع الجسيمات في الكتل وتختلف في الخواص الكمية الاخرى كالدوران المغزلي. وما ان مرت 4 سنوات منذ ظهور هذا التفسير حتى نجح التجريبيون في اصطياد اول جسيم مضاد وهو مضاد الالكترون او ما يعرف بـ “البوزترون”، واصبحت معادلة ديراك بصورة عامة بجانب معادلة كلين-جوردون تمثل حجر الاساس لما يعرف بنظرية المجال الكمي، حيث تهتم معادلة ديراك بوصف الفيرميونات (جسيمات تتبع توزريع احصائي يعرف بتوزيع فيرمي) وتهتم معادلة كلين-جوردون بوصف سلوك البوزونات القياسية (جسيم واحد يعرف بالهيغز بوزون يتبع احصاء بوز-اينشتاين).
بقلم: محمد ماهر عبد الرحيم محمد
بكالوريوس العلوم (مرتبة الشرف) في الفيزياء 2014- جامعة السودان للعلوم والتكنولوجيا






