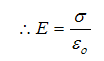محاضرة 9 فيزياء عامة (2) كهربية ساكنة أمثلة محلولة عن قانون جاوس
أمثلة محلولة عن قانون جاوس
Example 4.1
If the net flux through a gaussian surface is zero, which of the following statements are true?
1) There are no charges inside the surface.
2) The net charge inside the surface is zero.
3) The electric field is zero everywhere on the surface.
The number of electric field lines entering the surface equals the number leaving the surface.
Solution
Statements (b) and (d) are true. Statement (a) is not necessarily true since Gauss’ Law says that the net flux through the closed surface equals the net charge inside the surface divided by eo. For example, you could have an electric dipole inside the surface. Although the net flux may be zero, we cannot conclude that the electric field is zero in that region.
Example 4.2
A spherical gaussian surface surrounds a point charge q. Describe what happens to the: flux through the surface if
1) The charge is tripled,
2) The volume of the sphere is doubled,
3) The shape of the surface is changed to that of a cube,
The charge is moved to another position inside the surface;
Solution
1) If the charge is tripled, the flux through the surface is tripled, since the net flux is proportional to the charge inside the surface
2) The flux remains unchanged when the volume changes, since it still surrounds the same amount of charge.
3) The flux does not change when the shape of the closed surface changes.
4) The flux through the closed surface remains unchanged as the charge inside the surface is moved to another position. All of these conclusions are arrived at through an understanding of Gauss’ Law.
Example 4.3
A solid conducting sphere of radius a has a net charge +2Q. A conducting spherical shell of inner radius b and outer radius c is concentric with the solid sphere and has a net charge –Q as shown in figure 4.18. Using Gauss’s law find the electric field in the regions labeled 1, 2, 3, 4 and find the charge distribution on the spherical shell.
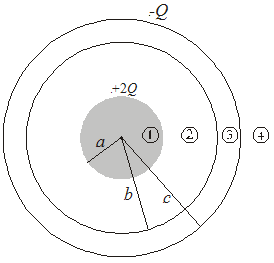
Figure 4.18
Solution
نلاحظ أن توزيع الشحنة على الكرتين لها تماثل كروي، لذلك لتعيين المجال الكهربي عند مناطق مختلفة فإننا سنفرض أن سطح جاوس كروي الشكل نصف قطره r.
Region (1) r < a
To find the E inside the solid sphere of radius a we construct a gaussian surface of radius r < a
E = 0 since no charge inside the gaussian surface.
Region (2) a < r < b
we construct a spherical gaussian surface of radius r
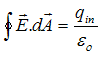
لاحظ هنا أن الشحنة المحصورة داخل سطح جاوس هي شحنة الكرة الموصلة الداخلية 2Q وأن خطوط المجال في اتجاه أنصاف الأقطار وخارجه من سطح جاوس أي q = 0 و المجال ثابت المقدار على السطح.
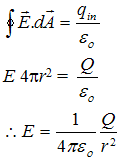
Region (4) r > c
we construct a spherical gaussian surface of radius r > c, the total net charge inside the gaussian surface is q = 2Q + (-Q) = +Q Therefore Gauss’s law gives
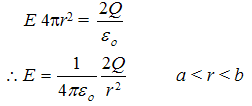 r > c
r > c
Region (3) b > r < c
المجال الكهربي في هذه المنطقة يجب أن يكون صفراً لأن القشرة الكروية موصلة أيضا، ولأن الشحنة الكلية داخل سطح جاوس b<r<c يجب أن تساوى صفراً. إذا نستنتج أن الشحنة –Qعلى القشرة الكروية هي نتيجة توزيع شحنة على السطح الداخلي والسطح الخارجي للقشرة الكروية بحيث تكون المحصلة –Q وبالتالي تتكون بالحث شحنة على السطح الداخلي للقشرة مساوية في المقدار للشحنة على الكرة الداخلية ومخالفة لها في الإشارة أي -2Qوحيث أنه كما في معطيات السؤال الشحنة الكلية على القشرة الكروية هي –Q نستنتج أن على السطح الخارجي للقشرة الكروية يجب أن تكون +Q
Example 4.4
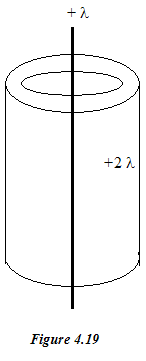
A long straight wire is surrounded by a hollow cylinder whose axis coincides with that wire as shown in figure 4.19. The solid wire has a charge per unit length of +λ, and the hollow cylinder has a net charge per unit length of +2λ. Use Gauss law to find (a) the charge per unit length on the inner and outer surfaces of the hollow cylinder and (b) the electric field outside the hollow cylinder, a distance r from the axis.
Solution
(a) Use a cylindrical Gaussian surface S1 within the conducting cylinder where E=0
 and the charge per unit length on the inner surface must be equal to
and the charge per unit length on the inner surface must be equal to
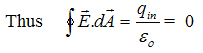
linner = -λ
Also linner + louter = 2λ
thus louter = 3λ
(b) For a gaussian surface S2 outside the conducting cylinder
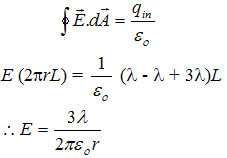
Example 4.5
Consider a long cylindrical charge distribution of radius R with a uniform charge density r. Find the electric field at distance r from the axis where r<R.
Solution
If we choose a cilindrical gaussian surface of length L and radius r, Its volume is πr2L, and it encloses a charge ρπr2L. By applying Gauss’s law we get,
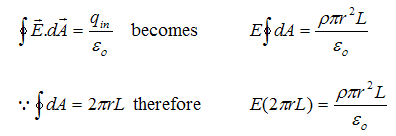
Thus
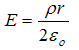 radially outward from the cylinder axis
radially outward from the cylinder axis
Notice that the electric field will increase as r increases, and also the electric field is proportional to r for r<R. For the region outside the cylinder (r>R), the electric field will decrease as r increases.
Example 4.5
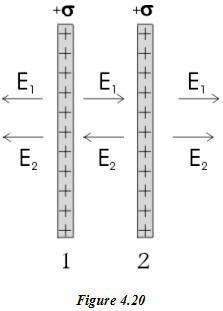 Two large non-conducting sheets of +ve charge face each other as shown in figure 4.20. What is E at points (i) to the left of the sheets (ii) between them and (iii) to the right of the sheets?
Two large non-conducting sheets of +ve charge face each other as shown in figure 4.20. What is E at points (i) to the left of the sheets (ii) between them and (iii) to the right of the sheets?
Solution
We know previously that for each sheet, the magnitude of the field at any point is
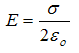
(a) At point to the left of the two parallel sheets
E = –E1 + (-E2) = -2E
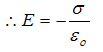
(b) At point between the two sheets
E = E1 + (-E2) = zero
(c) At point to the right of the two parallel sheets
E = E1 + E2 = 2E