محاضرة 8 مغناطيسية وتيار متردد
الحث الذاتي والطاقة المختزنة في المجال المغناطيسي والحث المتبادل
الحث الذاتي والطاقة المختزنة في المجال المغناطيسي والحث المتبادل: درسنا في المحاضرة السابقة ان التيار ينشئ في الدائرة الكهربية عندما يتغير الفيض المغناطيسي خلال الدائرة مع الزمن. وفي هذه المحاضرة سندرس الحث الذاتي Self Inductance الذي ينشئ في الدائرة نفسها عند مرور تيار كهربي فيها أو بمعنى ادق عند غلق او فتح الدائرة الكهربية. وهذا التأثير (الحث الذاتي) يلعب دوراً اساسياً في دوائر التيار المتردد حيث أن التيار يتغير باستمرار مع الزمن.
الحث الذاتي Self Inductance
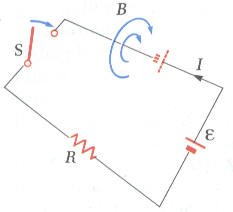
اعتبر دائرة كهربية مكونة من بطارية ومقاومة ومفتاح كهربي كما في الشكل المقابل، عند غلق فإن التيار المار في الدائرة سوف لن يصل إلى قيمته العظمى فور غلق المفتاح انما سوف يستغرق بعضا من الوقت نتيجة لقانون فارادي.كيف ذلك؟
عند غلق المفتاح في الدائرة الكهربية يحدث ما يلي:
- يزداد التيار المار في الدائرة مع الزمن.
- يزداد الفيض المغناطيسي خلال الدائرة نتيجة لازدياد التيار.
- الفيض المتزايد يؤدي إلى توليد قوة دافعة كهربية في الدائرة ليعاكس الزيادة في الفيض المغناطيسي. Lenz’s Law
هذه القوة الدافعة الكهربية المتولدة في الدائرة تعمل في عكس اتجاه التيار الأصلي وهذا نتج عن الزيادة في الفيض المغناطبيسي نتيجة لزيادة التيار عند غلق المفتاح… هذا التأثير في الدائرة يعرف باسم التأثير الحثي الذاتي Self Induction.
من قانون فارادي يمكننا من ايجاد صيغة رياضية للتعبير عن الحث الذاتي. حيث ان الفيض المغناطيسي يتناسب مع المجال المغناطيسي والاخير يتناسب مع التيار في الدائرة لذا فإن القوة الدافعة الكهربية للحث الذاتي تتناسب مع التغير في التيار الكهربي.
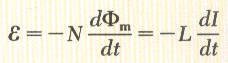
where L is a proportionality constant, called the inductance of the device.
الحث الذاتي L في المغناطيسية يناظر السعة الكهربية C. ويمكن التعبير عن الحث الذاتي L بالابعاد الهندسية للدائرة. فإذا افترضنا ملف عدد لفاته N فإن L تعطى بالعلاقة التالية:
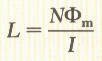
كما يمكن التعبير عن الحصث الذاتي بالمعادلة التالية:
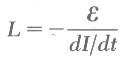
وهذه المعادلة تعطي قيمة الحث الذاتي للدائرة بغض النظر عن ابعادها الهندسية وانما تعتمد على قياس الميات الفيزيائية مثل القوة الدافعة الكهربية والتغيير في التيار. وتكون وحدة الحث الذاتي هي الهنري Henry.
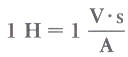
كيف يمكن ايجاد الحث الذاتي من خلال قياس الابعاد الهندسية
اعتبر ملف عدد لفاته N لفة وطوله l اكبر بكثير من نصف قطر الملف. ينشأ عنه مجالاً مغناطيسياً يعطى بالعلاقة التالية:
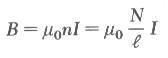 اما الفيض الكهربي فيعطى بالعلاقة التالية:
اما الفيض الكهربي فيعطى بالعلاقة التالية:
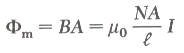
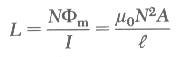
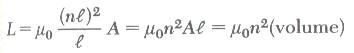
ومن هذا يتضح ان الحث الذاتي للملف يعتمد على خواصه الهندسية (الطول والمساحة وعدد اللفات).
الطاقة المختزنة في المجال المغناطيسي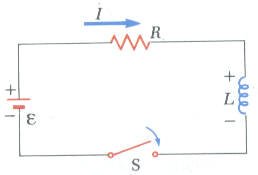
درسنا في مقرر الفيزياء العامة 2 الكهربية الساكنة ووجدنا ان المجال الكهربي في الفراغ هو عبارة عن طاقة كهربية في صورة مجال. كذلك الحال بالنسبة للمجال المغناطيسي. ولاثبات علاقة الطاقة المختزنة بالمجال المغناطيسي افترض الدائرة الكهربية الموضحة في الشكل المقابل، بتطبيق قاعدة كيرشوف الثانية على التغير في فرق الجهد على كل عنصر من عناصر الدائرة الكهربية ينتج أن:
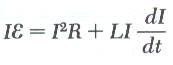
باعادة ترتيب المعادلة والضرب في التيار I ينتج أن
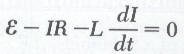
تدل المعادلة السابقة على أن الطاقة التي تبذلها البطارية Iε تساوي مجموع الطاقة المبددة على شكل طاقة حرارية في المقاومة I2R والطاقة المختذنة في الملف ![]() . وعليه يمكن التعبير عن التغير في الطاقة المختذنة في الملف بالصورة التالية:
. وعليه يمكن التعبير عن التغير في الطاقة المختذنة في الملف بالصورة التالية:
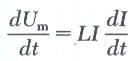
ولايجاد الطاقة الكلية المختزنة في الملف نجري عملية التكامل
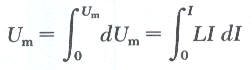
![]() *
*
وهذه المعادلة تعطي الطاقة الكلية المختزنة في الملف.
ماذا عن كثافة الطاقة؟
يمكن حساب الطاقة المختزنة في المجال المغناطيسي لكل وحدة حجوم وهو المقصود بكثافة الطاقة، اعتبر ملف حثه الذاتي والمجال المغناطيسي له يعطى بالمعادلتين
![]()
![]()
بالتعويض عن التيار I والحث الذاتي للملف L في المعادلة *
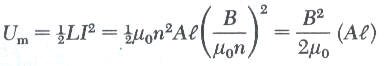
بالقسمة على الحجم للحصول على كثافة الطاقة نصل إلى المعادلة التالية:
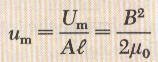
وهذه المعادلة تعطي كثافة الطاقة لكل وحدة حجوم لأي مجال مغناطيسي.
الحث المتبادل Mutual Inductance
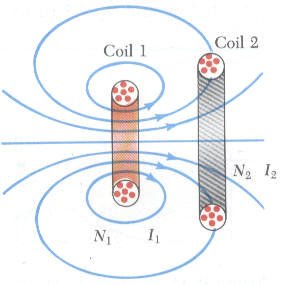
نتيجة للتغير في التيار الكهربي في دائرة يؤدي إلى تغيير في الفيض المغناطيسي في دائرة كهربية مجاورة. وهذا بالتأكيد يولد قوة دافعة كهربية في تلك الدائرة ويسمي هذا التأثير بالتأثير الحثي المتبادل Mutual Inductance لأنه نتج من تأثير دائرة كهربية على اخرى.
في الشكل المقابل توضيح للتأثير الحثي المتبادل حيث ملفين متجاورين يمر في الملف الأول وعدد لفاته N1 تيار كهربي قيمته I1 ينشئ مجالا مغناطيسياً يؤثر على الملف الثاني وعدد لفاته N2 بفيض مغناطيسي F21 يؤدي إلى تيار حثي في الملف الثاني وقيمته I2.
يعرف التأثير الحثي المتبادل M21 في الملف الثاني من خلال المعادلة التالية:
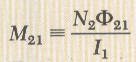
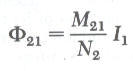
إذا كان التيار I1 في الملف الأول متغير مع الزمن فإن من قانون فارادي تكون القوة الدافعة الكهربية المتولدة في الملف الثاني نتيجة للملف الأول هي:
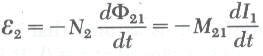
وبنفس الفكرة إذا كان التيار I2 في الملف الثاني متغير مع الزمن فإن من قانون فارادي تكون القوة الدافعة الكهربية المتولدة في الملف الأول نتيجة للملف الثاني هي:
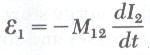
أي ان القوة الدافعة الكهربية المتولدة في ملف تتناسب طردياً من معدل التغير في التيار الكهربي في الملف الآخر.
حالة خاصة:
في حالة ما يكون معدل التغير في التيار dI1/dt=dI2/dt فإن القوة الدافعة الكهربية
ε1 = ε2
وهذا يعني أن
M21=M12=M
وتكون قيمة القوة الدافعة الكهربية في الملفين تعطى بـ
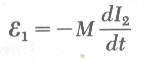
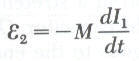
وتكون وحدة الحث المتبادل هي الهنري Henry


