من المحاضرات السابقة تم التعامل مع كتلة النواة على انها كبيرة جداً اي لا نهائية الكتلة بالمقارنة مع كتلة الإلكترون وتم التعامل مع كتلة النواة على انها ثابتة ولا تتحرك في الفراغ. وهذا تقريب جيد يمكن استخدامه لذرة الهيدروجين التي تحتوي على اقل كتلة نواة وان هذه الكتلة تساوي 2000 مرة كتلة الإلكترون. ولكن من نتائج القياسات الطيفية المنبعثة من من ذرة الهيدروجين والتي تكون دقيقة للغاية فإنه بمقارنة نتائج هذه القياسات مع القيم المتوقعة من فرضية لوهر لذرة الهيدروجين نجد أن هناك اختلاف قليل بين القياسات العملية والقيم المتوقعة من فرضية بوهر وهذا أدى إلى انه يجب التعامل مع كتلة النواة على انها محدودة وان كل من الإلكترون والنواة تتحركان حول مركز ثقل كتلة الذرة كما في حالة حركة الكواكب. وهنا سوف نعتبر ان الإلكترون يتحرك بالنسبة للنواة كما لو ان الكتلة النواة ثابتة وان كتلة الإلكترون m قد اختزلت إلى قيمة m تسمى الكتلة المختزلة Reduced Mass للذرة وعليه سوف نتعامل مع كتلة الإلكترون على أنها هي الكتلة المختزلة والتي تعطى بالعلاقة التالية:
![]()
where M is the mass of the nucleus and m is the mass of the electron
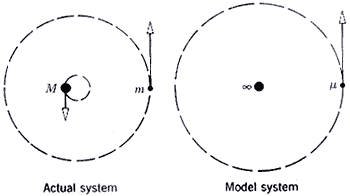
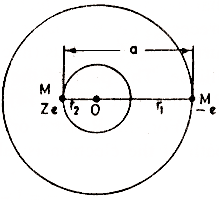
ولاثبات هذه العلاقة نفترض ان كلاً من الإلكترون والنواة تدوران حول مركز الثقل الموضح بالشكل المبين O حيث ان نصف قطر دوران الإلكترون حول مركز الثقل هو r1 وان نصف قطر دوران النواة حول مركز الثقل هو r2 ومن نظرية مركز الثقل نعلم ان Mr2=mr1 فإذا كان aتمثل المسافة بين النواة والإلكترون.
r1 = a – r2 = a – mr1/M (1)
r1 = aM/(M+m)
and
r2 = mr1/M = am/(M+m) (2)
وحيث أن الكتلتين تدوران في مسار دائري فإن قوة التجاذب تتساوى مع قوة الطرد المركزي لكل من الكتلتين.
| For the Nucleus | |
| For the electron |
ومن حساب طاقة الحركة لكل من الإلكترون والنواة نجد ان
Total K.E. = 1/2 mv2 + 1/2 MV2
where v = wr1 and V = wr2
there for the total K.E. = 1/2 mw2r12 + 1/2 Mw2r22
بالتعويض في المعادلة السابقة عن r1 و r2 بالمعادلتين (1) و (2) نحصل على
![]()
![]()
therefore,
![]()
وهذه هي الكتلة المختزلة reduced mass وهي اقل من كتلة الإلكترون بـ
1/(1+m/M)
تعديل نموذج بوهر ليأخذ في الحسبان الكتلة المختزلة
مما سبق مناقشته فإن الفرضية الثاني لنموذج بوهر والمتعلقة بال العزم الزاوي للذرة orbital angular momentum L تصبح بالصورة التالية:
![]()
حيث تم استبدال كتلة الإلكترون بالكتلة المختزلة.
وبعمل هذا الاستبدال لكتلة الإلكترون بالكتلة المختزلة في كل المعادلات التي حصلنا عليها من فرضيات بوهر لتصحيح افتراض بوهر ان كتلة النواة لانهائية فإننا سنحصل على النفس معادلات بوهر مع استبدال كتلة الإلكترون بالكتلة المختزلة وبالتركيز على معادلة مقلوب الطول الموجي للطيف المنبعث من الذرة فإنها تصبح على النحو التالي:
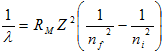
where
![]()
في الأمثلة التالية سوف يتضح تأثير التعامل مع الكتلة المختزلة على ذرات شبيهة بذرة الهيدروجين على الطيف المنبعث وعلى مستويات الطاقة.
Example
Consider a positronium atom consisting of a positron and electron revolving about their common center of mass half way between them, If such a system were a normal atom (a) How would its emission spectrum compare to that of the hydrogen atom? (b) What would be the radius of the ground state orbit of positronium?
نحسب الكتلة المختزلة لهذه الذرة
![]()
نحسب ثابت ريدبيرج لهذه الذرة
![]()
تكون مستويات الطاقة من معادلة بوهر هي
![]()
تكون المعادلة التي تعطي مقلوب الأطوال الموجية لطيف ذرة البوزيترونيوم هي
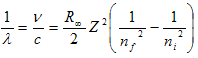
وهذا يعني ان التردد المنبعث يكون اقل بمقدار النصف بالمقارنة بتردد طيف ذرة الهيدروجين او ان الطول الموجي يكون ضعف الطول الموجي المقابل له في ذرة الهيدروجين.
اما بالنسبة لنصف قطر المدار الأول
![]()
وهذا يعني ان نصف قطر المدار الأول في ذرة البوزيترونيوم اكبر بمقدار مرتين منه في ذرة الهيدروجين.
Example
A muonic atom contains a nucleus of charge Ze and a negative muon moving about it. The muon is an elementary particle with charge -e and a mass is 207 times as large as an electron mass. Such an atom is formed when a proton captures a muon. (a) Calculate the raduis of the first Bohr orbit of a muonic atom with Z=1. (b) Calculate the binding energy of muonic atom with Z=1. (c) What is the wavelength of the first line in the Lyman series for such an atom?
حيث ان كتلة النواة هي 1836 كتلة الإلكترون وكتلة الميون 207 كتلة الإلكترون فإن الكتلة المختزلة لذرة muonic
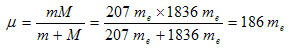
بالتعويض عن كتلة الإلكترون في معادلة بوهر التي تحسب نصف قطر المدار بالكتلة المختزلة نحصل على
![]()
وهذا يعني ان الميون يدور في مدار قريب جداً من النواة.
اما بالنسبة لطاقة الربط لذرة muonic تكون
![]()
وهذه طاقة ربط كبيرة جداً بالمقارنة بطاقة الربط في ذرة الهيدروجين.
أما بالنسبة للطول الموجي الأول في سلسلة Lyman فهي تحسب من معادلة ريدبيرج
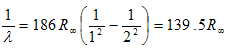
بالتعويض عن ni=2 و nf=1 .
R∞=109737cm-1
l =6.5Å
وهذا يعني ان الخط الطيفي الأول في سلسلة Lymen لذرة muonic يقع فى مجال طيف اشعة اكس.
Example
Deuterium atom is a hydrogen atom whose nucleus contains a proton and a neutron. How does the doubled nuclear mass affect the atomic spectrum?
اذا لم نكن نستخدم الكتلة المختزلة لتوقعنا ان الطيف المنبعث من ذرة الهيدروجين وذرة الديتيريوم متطابقين ولكن في حالة ذرة الديتيريوم فإن كتلة النواة ضعف كتلة نواة ذرة الهيدروجين وهذا سوف يؤدي إلى اختلاف الطيف المنبعث عن كلا الذرتين. من خلال حساب ثابت رايدبيرج في حالة ذرة الهيدروجين نجد ان
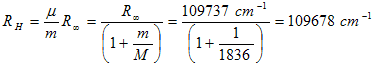
أما في حالة ذرة الديتيريوم فإن ثابت ريدبيرج يكون
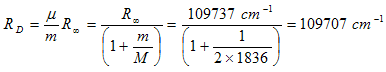
ومن مقارنة القيمتين نجد أن RD أكبر من RH وهذا يؤدي إلى الاستنتاج بأن طيف ذرة الديتيريوم سيكون مزاح ناحية اطوال موجية اقل.
ملاحظة:
تم اكتشاف الديتيريوم في 1932 بواسطة العالم Urey عند ملاحظة ازاحة للخطوط الطيفية المنبعثة من غاز الهيدروجين لوجود نسبة 1:6000 هيدروجين إلى ديتيريوم في الطبيعة.


