محاضرة 4 فيزياء عامة (2) كهربية ساكنة
التدفق الكهربي Electric Flux وقانون جاوس Gauss’s law
درسنا سابقا كيفية حساب المجال لتوزيع معين من الشحنات باستخدام قانون كولوم. وهنا سنقدم طريقة أخرى لحساب المجال الكهربي باستخدام “قانون جاوس” الذي يسهل حساب المجال الكهربي لتوزيع متصل من الشحنة على شكل توزيع طولي أو سطحي أو حجمي. يعتمد قانون جاوس أساساً على مفهوم التدفق الكهربي الناتج من المجال الكهربي أو الشحنة الكهربائية، ولهذا سنقوم أولاً بحساب التدفق الكهربي الناتج عن المجال الكهربي، وثانياً سنقوم بحساب التدفق الكهربي الناتج عن شحنة كهربية، ومن ثم سنقوم بإيجاد قانون جاوس واستخدامه في بعض التطبيقات الهامة في مجال الكهربية الساكنة.
4.1 The Electric Flux due to an Electric Field
We have already shown how electric field can be described by lines of force. A line of force is an imaginary line drawn in such a way that its direction at any point is the same as the direction of the field at that point. Field lines never intersect, since only one line can pass through a single point.
The Electric flux (F) is a measure of the number of electric field lines penetrating some surface of area A.
Case one:
The electric flux for a plan surface perpendicular to a uniform electric field
To calculate the electric flux we recall that the 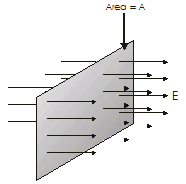 number of lines per unit area is proportional to the magnitude of the electric field. Therefore, the number of lines penetrating the surface of area Ais proportional to the product EA. The product of the electric filed E and the surface area Aperpendicular to the field is called the electric flux F.
number of lines per unit area is proportional to the magnitude of the electric field. Therefore, the number of lines penetrating the surface of area Ais proportional to the product EA. The product of the electric filed E and the surface area Aperpendicular to the field is called the electric flux F.
![]()
The electric flux F has a unit of N.m2/C.
Case Two
The electric flux for a plan surface make an angle q to a uniform electric field
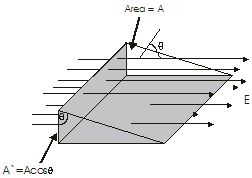 Note that the number of lines that cross-area is equal to the number that cross the projected area A`, which is perpendicular to the field. From the figure we see that the two area are related by A`=Acosθ. The flux is given by:
Note that the number of lines that cross-area is equal to the number that cross the projected area A`, which is perpendicular to the field. From the figure we see that the two area are related by A`=Acosθ. The flux is given by:
![]() = E A cosθ →
= E A cosθ → ![]()
Where θ is the angle between the electric field E and the normal to the surface ![]()
إذاً يكون الفيض ذا قيمة عظمى عندما يكون السطح عمودياً على المجال أي θ = 0 ويكون ذا قيمة صغرى عندما يكون السطح موازياً للمجال أي عندما θ = 90. لاحظ هنا أن المتجه هو متجه المساحة ![]() وهو عمودي دائما على المساحة وطوله يعبر عن مقدار المساحة.
وهو عمودي دائما على المساحة وطوله يعبر عن مقدار المساحة.
Case Three
In general the electric field is nonuniform over the surface
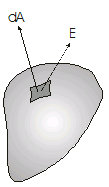 The flux is calculated by integrating the normal component of the field over the surface in question.
The flux is calculated by integrating the normal component of the field over the surface in question.
The net flux through the surface is proportional to the net number of lines penetrating the surface
![]()
![]()
والمقصود بـ net number of lines أي عدد الخطوط الخارجة من السطح (إذا كانت الشحنة موجبة) – عدد الخطوط الداخلة إلى السطح (إذا كانت الشحنة سالبة).
Example 4.1
What is electric flux F for closed cylinder of radius R immersed in a uniform electric field as shown in figure?
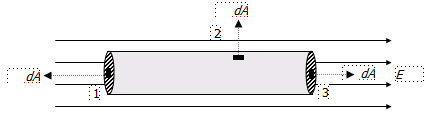
Solution
نطبق قانون جاوس على الأسطح الثلاثة الموضحة في الشكل أعلاه
![]()
![]()
Since E is constant then
F = – EA + 0 + EA = zero
Exercise
Calculate the total flux for a cube immersed in uniform electric field ![]() .
.
4.2 The Electric Flux due to a point charge
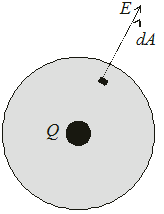
To calculate the electric flux due to a point charge we consider an imaginary closed spherical surface with the point charge in the center figure 4.5, this surface is called gaussian surface. Then the flux is given by
(θ = 0) ![]()
![]()
![]() (4.3)
(4.3)
Note that the net flux through a spherical gaussian surface is proportional to the charge q inside the surface.
4.3 Gaussian surface
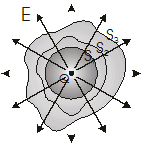 Consider several closed surfaces as shown in figure 4.6 surrounding a charge Q as in the figure below. The flux that passes through surfaces S1, S2 and S3 all has a value q/εo. Therefore we conclude that the net flux through any closed surface is independent of the shape of the surface.
Consider several closed surfaces as shown in figure 4.6 surrounding a charge Q as in the figure below. The flux that passes through surfaces S1, S2 and S3 all has a value q/εo. Therefore we conclude that the net flux through any closed surface is independent of the shape of the surface.
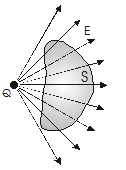 Consider a point charge located outside a closed surface as shown in figure 4.7. We can see that the number of electric field lines entering the surface equal the number leaving the surface. Therefore the net electric flux in this case is zero, because the surface surrounds no electric charge.
Consider a point charge located outside a closed surface as shown in figure 4.7. We can see that the number of electric field lines entering the surface equal the number leaving the surface. Therefore the net electric flux in this case is zero, because the surface surrounds no electric charge.
Example 4.2
In figure 4.8 two equal and opposite charges of 2Q and -2Q what is the flux F for the surfaces S1, S2, S3 and S4.
Solution
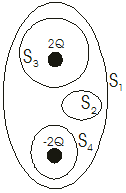
For S1 the flux F = zero
For S2 the flux F = zero
For S3 the flux F = +2Q/ εo
For S4 the flux F = -2Q/ εo
4.4 Gauss’s Law

Gauss law is a very powerful theorem, which relates any charge distribution to the resulting electric field at any point in the vicinity of the charge. As we saw the electric field lines means that each charge q must have q/eo flux lines coming from it. This is the basis for an important equation referred to as Gauss’s law. Note the following facts:
1. If there are charges q1, q2, q3, ……qn inside a closed (gaussian) surface, the total number of flux lines coming from these charges will be
(q1 + q2 + q3 + ……. +qn)/εo (4.4)
- The number of flux lines coming out of a closed surface is the integral of
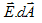 over the surface,
over the surface, 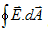
We can equate both equations to get Gauss law which state that the net electric flux through a closed gaussian surface is equal to the net charge inside the surface divided by eo
Gauss’s law ![]() (4.5)
(4.5)
where qin is the total charge inside the gaussian surface.
Gauss’s law states that the net electric flux through any closed gaussian surface is equal to the net electric charge inside the surface divided by the permittivity.
4.5 Gauss’s law and Coulomb’s law
 We can deduce Coulomb’s law from Gauss’s law by assuming a point charge q, to find the electric field at point or points a distance r from the charge we imagine a spherical gaussian surface of radius r and the charge q at its center as shown in figure 4.10.
We can deduce Coulomb’s law from Gauss’s law by assuming a point charge q, to find the electric field at point or points a distance r from the charge we imagine a spherical gaussian surface of radius r and the charge q at its center as shown in figure 4.10.![]()
![]() Because E is constant for all points on the sphere, it can be factored from the inside of the integral sign, then
Because E is constant for all points on the sphere, it can be factored from the inside of the integral sign, then
![]() →
→ ![]() →
→ ![]()
![]() (4.6)
(4.6)
Now put a second point charge qo at the point, which E is calculated. The magnitude of the electric force that acts on it F = Eqo
![]()


