محاضرة 12 فيزياء الليزر انقلاب التعداد Population Inversion
انقلاب التعداد Population Inversion
انقلاب التعداد شرط رئيسي لعملية الانبعاث الاستحثاثي stimulated emission اللازم لتكبير الضوء، وانقلاب التعداد هو توزيع للذرات على مستويات الطاقة مختلف على التوزيع في حالة الاتزان الحراري thermal equilibrium الخاضع لاحصائيات قانون ماكسويل بولتزمان ولتوضيح فكرة انقلاب التعداد سوف نقوم بشرح مختصر للتوزيع في حالة الاتزان الحراري.
Thermal Equilibrium
From thermodynamics we know that a collection of atoms, at a temperature T [0K], in thermodynamic equilibrium with its surrounding, is distributed so that at each energy level there is on the average a certain number of atoms.
The number of atoms (Ni) at specific energy level (Ei) is called Population Number.
The Boltzmann equation determines the relation between the population number of a specific energy level and the temperature:
Ni = const * exp (-Ei/kT)
Ni = Population Number = number of atoms per unit volume at certain energy level Ei.
k = Boltzmann constant: k = 1.38*1023 [Joule/0K].
Ei = Energy of level i. We assume that Ei> Ei-1.
Const = proportionality constant. It is not important when we consider population of one level compared to the population of another level.
T = Temperature in degrees Kelvin [0K] (Absolute Temperature).
The Boltzmann equation shows the dependence of the population number (Ni) on the energy level (Ei) at a temperature T.
From this equation we see that:
1. The higher the temperature, the higher the population number.
2. The higher the energy level, the lower the population number.
الاتزان الحراري
عند درجات الحرارة المنخفضة تكون كل الذرات في المستوى الأرضي وبزيادة درجة الحرارة (بتحريك المؤشر لليمين تثار الذرات لمستويات طاقة اعلى وهذا خاضع لقانون ماكسويل بولتزمان الاحصائي عند الاتزان الحراري.
Relative Population (N2/N1)
The relative population (N2/N1) of two energy levels E2 compared to E1 is:
N2/N1 = const* exp (-E2/kT)/ const* exp (-E1/kT)
N2/N1 = exp(-(E2-E1)/kT)
The proportionality constant (const) is canceled by division of the two population numbers.
|
|
The Figure below shows the population of each energy level at thermal equilibrium.
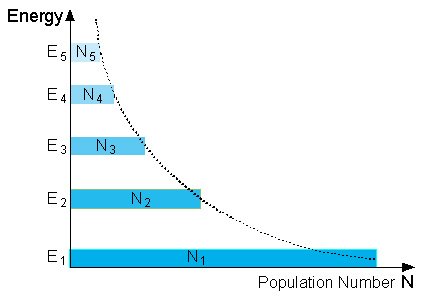
Population Numbers at “Normal Population”
Example
Calculate the ratio of the population numbers (N1, N2) for the two energy levels E2 and E1 when the material is at room temperature (3000K), and the difference between the energy levels is 0.5 [eV]. What is the wavelength (l) of a photon which will be emitted in the transition from E2 to E1?
Solution
When substituting the numbers in the equation, we get:
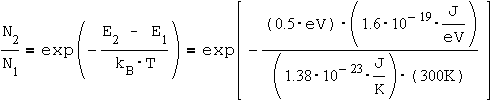
= 4 * 10-9
ومن هذه النتيجة يتبين لنا أنه عند درجة حرارة الغرفة يكون التعداد في مستوي الطاقة الأرضي ground level الف مليون ذرة في حين التعداد في المستوي الأول excited state 4 ذرات فقط!!!
To calculate the wavelength:
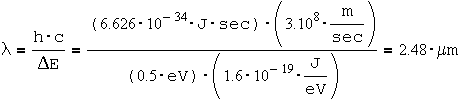
This wavelength is in the Near Infra-Red (NIR) spectrum.
Population Inversion
We saw that in a thermal equilibrium Bolzman equation shows us that :
N1 > N2 > N3
Thus, the population numbers of higher energy levels are smaller than the population numbers of lower ones.
This situation is called “Normal Population“. In a situation of normal population a photon impinging on the material will be absorbed, and raise an atom to a higher level.
By putting energy into a system of atoms, we can achieve a situation of “Population Inversion“. In population inversion, at least one of the higher energy levels has more atoms than a lower energy level.
An example is described in the Figure below. In this situation there are more atoms (N3) in an higher energy level (E3), than the number of atoms (N2) in a lower energy level (E2).
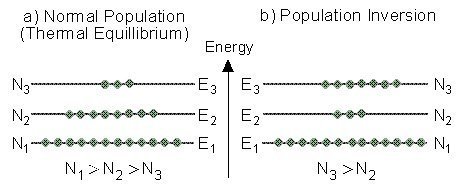
“Normal Population” compared to “Population Inversion”.
The process of raising the number of excited atoms is called “Pumping“.
Three Level Laser
A schematic energy level diagram of a laser with three energy levels is the figure below.
The two energy levels between which lasing occur are: the lower laser energy level (E1), and the upper laser energy level (E2).
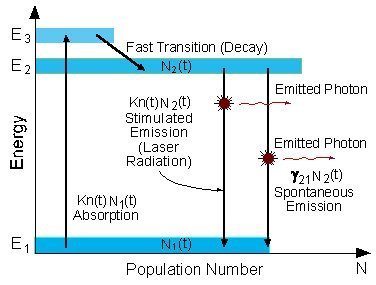
Energy level diagram in a three level laser
To achieve lasing, energy must be pumped into the system to create population inversion. So that more atoms will be in energy level E2 than in the ground level (E1).
Atoms are pumped from the ground state (E1) to energy level E3. They stay there for an average time of 10-8 [sec], and decay (usually with a non-radiative transition) to the meta-stable energy level E2.
Since the lifetime of the meta-stable energy level (E2) is relatively long (of the order of 10-3 [sec], many atoms remain in this level.
If the pumping is strong enough, then after pumping more than 50% of the atoms will be in energy level E2, a population inversion exists, and lasing can occur.
Question
The condition of high pumping, limits the operation of a three level laser to pulsed operation. Why is continuous operation impossible in a three level laser?
Four Level Laser
The schematic energy level diagram of a four level laser is shown in the figure below.
Compared to the equivalent diagram of a three level laser, there is an extra energy level above the ground state. This extra energy level has a very short lifetime.
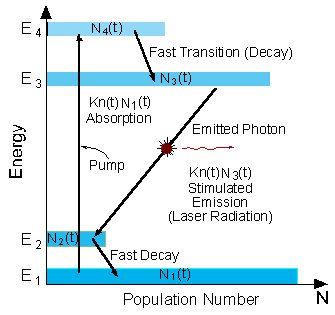
Energy level diagram in a four level laser
The pumping operation of a four level laser is similar to the pumping of a three level laser. This is done by a rapid population of the upper laser level (E3), through the higher energy level (E4).
The advantage of the four level laser is the low population of the lower laser energy level (E2).
To create population inversion, there is no need to pump more than 50% of the atoms to the upper laser level.
The population of the lower laser level (N2(t)) is decaying rapidly to the ground state, so practically it is empty. Thus, a continuous operation of the four level laser is possible even if 99% of the atoms remain in the ground state (!)
Advantages of four level lasers Compared to three level lasers:
-
The lasing threshold of a four level laser is lower.
-
The efficiency is higher.
-
Required pumping rate is lower.
-
Continuous operation is possible.
Summary
-
In a three level laser the lower laser level is the ground state.
-
In a four level laser the lower laser level is above the ground state.



