In the classical mechanics (Galilean transformation) the velocity can be added or subtracted, but this contradicts with the first postulate of the special relativity since the maximum speed is the speed of light. The question is what is the velocity of a pulse of light sent from a spacecraft travelling at speed 0.8c? According to the (Galilean transformation equations of velocity is 1.8c. However, this is not valid in Einstein’ postulate. Einstein said
The velocity of light forms the upper limits of velocities for all material bodies… The simple mechanical laws of adding and subtracting velocities is no longer valid, or more precisely, is approximately valid for small velocities, but not for those near the velocity of light.
A. Einstein and L. Infeld, The Evolution of Physics (1938)
Once we have the Lorentz transformation for distance and time, is a straightforward matter to consider the time derivatives of displacements as measured hi two different frames of reference. Consider the following example
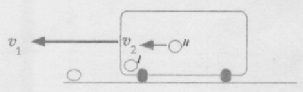
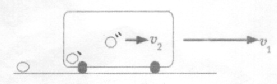Suppose that one of the passenger of the boxcar is running with speed v2 w.r.t observer O’ and the boxcar is travelling with speed v1 w.r.t the observer O. What is the speed v of O” w.r.t O?
In classical mechanics one would say that the speed of O” w.r.t. O is simply v1+v2 However, this is not correct in the Einstein’s mechanics. From equations (3) & (4)
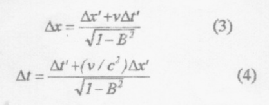
Lets assume that the speed of O” w.r.t O is v = Δx/Δt
the speed of O” w.r.t O’ is v2 = Δx’/Δt’ and the speed of O’ w.r.t O is v1
Dividing equations (3) & (4)
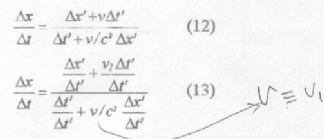
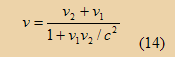
If we assume that a light pulse was replaced the O” the its speed w.r.t O according to equation (14) is
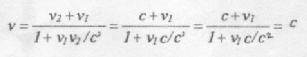
نلاحظ ان الموجة الضوئية سرعتها بالنسبة للمراقبين ’O’’ & O هي سرعة الضوء بدون اي تأثير لسرعة العربة وهذا متفق مع فروض النظرية النسبية.
If v2 in the previous example was opposite to the direction of v then equation (14) become
(15) 
If v2 and v1 in the previous example were both in the opposite direction then equation (14) become
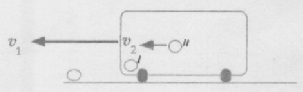
(16)
أي أن السرعة لها نفس القيمة ولكن في الاتجاه المعاكس للحالة الأولى
ملاحظة
نلاحظ من المعادلات السابقة 14 و 15 و16 إنه إذا كانت السرعات التي نتعامل معها صغبرة بالمقارنة بسرعة الضوء وبالتالي يصبح المقام في المعادلات السابقة مساوياً للوحدة وبهذا التقريب نحصل على معادلة جاليلو لجمع السرعات.
Example
A spaceship travelling with speed of 95% of the speed of light w.r.t, the earth If this spaceship overtake another spaceship travelling with speed of 90% ot’ the speed of light w earth as wcll. What is the speed of each spaceship measured by the observers in both ships?
Solution
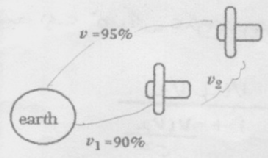
B=0.95 B1 = 0.90 and B2 = v2/c
From equation (14)
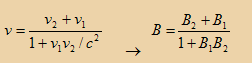
B(1+B1B2) = B1+B2
(0.95)(1+0.90B2)=0.90+B2
B2 = 0.345
v2 = 0.345c
لمراقب على الأرض يجد أن فرق السرعتين 5% ولكن بالنسبة لاحدهما يجد ان سرعة الآخر 34.5%
