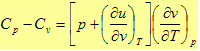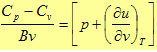تعرف الطاقة الداخلية لعينة نقية من المادة في حالة اتزان حراري من خلال دالة في الضغط والحجم ودرجة الحرارة وتعرف هذه الدالة بمعادلة الطاقة الداخلية اي ان
u=f(p,v,T)
وحيث ان هناك علاقة رياضية تربط بين كلا من الضغط والحج ودرجة الحرارة فإن معادلة الطاقة يمكن ان تكون دالة من متغييرين فقط مثل
u=f(p,v) or u=f(v,T) or u=f(p,T)
في هذه المحاضرة سوف نكتفي بإيجاد كعادلة الطاقة من خلال الدالة (v,T) لنحصل على بعض المفاهيم الأساسية في علم الديناميكا الحرارية كما يمكن للطالب ان يدرس علاقة معادلة الطاقة مع متغييرين اخرين وذلك بنفس الفكرة التي سيتم شرحها.
u=f(v,T) Spacific heat of a gas السعة الحرارية للغاز
اعتبر دالة الطاقة u كدالة في المتغييرين الحجم ودرجة الحرارة أي ان
u=f(v,T) (1)
وبإجراء التفاضل للمعادلة نحصل على
![]() (2)
(2)
ومن القانون الأول للديناميكا الحرارية
dQ=du+dW
where dW = pdv
therefore dQ = du+pdv
بالتعويض في المعادلة (2) نحصل على
![]() (3)
(3)
بالقسمة على dT نحصل على
![]()
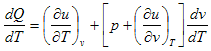 (4)
(4)
من المعادلة (4) سوف نحصل على بعض المفاهيم التالية:
حالة خاصة (1) لعملية عند ثبوت الحجم Isochoric process
يكون التغير في الحجم مساوياً للصفر أي dv=0 وبتطبيق ذلك على المعادلة (4) نحصل على
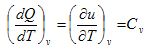 (5)
(5)
وهذا يضيف مفهوم جديد للسعة الحرارية التي عرفت سابقاً على انها مقدار كمية الحرارة اللازمة لرفع درجة حرارة المادة درجة مئوية أو انها التغير في كمية الحرارة بالنسبة لدرجة الحرارة عند ثبوت الحجم. ومن معادلة الطاقة نجد ان السعة الحرارية عند ثبوت الحجم تساوي التغير في الطاقة الداخلية للمادة بالنسبة لدرجة الحرارة عند ثبوت الحجم.
حالة خاصة (2) لعملية عند ثبوت الضغط Isobaric process
يكون التغير في الضغط مساوياً للصفر أي dp=0 وبتطبيق ذلك على المعادلة (4) مع العلم بأن السعة الحرارية عند ثبوت الضغط تساوي التغير في كمية الحرارة بالنسبة لدرجة الحرارة
![]()
وبالتعويض في المعادلة (4) نحصل على
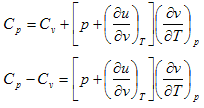 (6)
(6)
نلاحظ أن كل الكميات في الطرف الأيمن من المعادلة (6) تحسب من معادلة الحالة والكميات في الطرف الأيسر يمكن ايجادها عمليا (بالتجربة)
لنطبق المعادلة (6) على غاز مثالي معزول Isolated Ideal Gas بحيث ان التغير في كمية الحرارة والشغل يساويان صفر وبالتالي التغير في الطاقة الداخلية يسوي صفر.
dW & dQ = 0 therefore du = 0
وهذا يؤدي إلى أن الحد ![]() وبتطبق ذلك في المعادلة (6) نحصل على
وبتطبق ذلك في المعادلة (6) نحصل على
![]() (7)
(7)
الطرف الأيمن من المعادلة هو الثابت العام للغازات R ويمكن التحقق من ذلك من خلال معادلة الحالة للغاز المثالي أذا نحصل على العلاقة الهامة التالية:
Cp-Cv = R
أي أن الفرق بين السعة الحرارية عند ثبوت الضغط والسعة الحرارية عند ثبوت الحجم يساوي مقدار ثابت وهو الثابت العام للغازات R.
حالة خاصة (3) لعملية عند ثبوت درجة الحرارة Isothermal process
علمنا سابقاً أن العملية التي تتم عند ثبوت درجة الحرارة مع وجود تسخين هي تلك العمليات التي تحدث عن تحول المادة مصورة إلى اخرى مثل تحول الصلب إلى سائل أو تحول السائل إلى بخار وهنا تكون دذجة الحرارة ثابتة بالرغم من قيامنا بتزويد حرارة للنظام ولفهم ماذا يحدث للطاقة الداخلية سنعوض في المعادلة (3) عن dT=0 لنحصل على
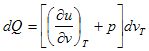 (8)
(8)
وهذا يوضح أن التغير في كمة الحرارة dQ في حالة ثبوت درجة الحرارة فإن جزء من كمية الحرارة يعمل على زيادة الطاقة الداخلية للمادة المتحولة بالنسبة للحجم والجزء الأخر من كمية الحرارة يبذل شغل وهذا الشغل بالتأكيد لزيادة المسافة بين جزيئات المادة ولهذا السبب لا يطرأ أزدياد في درجة الحرارة.
كما أن المعادلة لا نحتاج إلى تعريف السعة الحرارية عند ثبوت درجة الحرارة لأنها تساوي مالانهية أي أن النظام في حالة ثبوت درجة الحرارة يتصرف كما لو كانت سعته الحرارية لا نهائية لان اي كمية حرارة تزود الى النظام لن تؤدي إلى رفع درجة حرارته.
حالة خاصة (4) لعملية عند ثبوت كمية الحرارة Adiabatic process
في العملية الأديباتيكية هي التي تتم عند ثبوت كمية الحرارة وتحدث لنظام معزول فلا يمكن ان تتسرب الحرارة منه او إليه وبالتالي نقول أن dQ=0 وبالتعويض عن ذلك في المعادلة (4) نحصل على
![]()
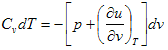
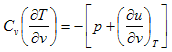 (9)
(9)
|
معامل التمدد الحجمي عند ثبوت الضغط يعطى بالعلاقة التالية:
حيث B هي معامل التمدد الحجمي، ومن المعادلة (6)
وفي حالة عملية تتم على غاز مثالي في نظام معزول يكون التغير في الطاقة الداخلية بالنسبة للحجم عند ثبوت درجة الحرارة يساوي صفر
إذا نحصل على
|
بالتعويض في المعادلة (9) نحصل على
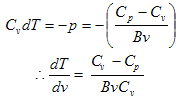 (12)
(12)
Experimental determination of heat capacities
(1) For all gases
Cv is a function of T
Cp is a function of T
Cp-Cv = Constant = R
γ=Cp/Cv is a function of T and g>1
(2) For mono-atomic gases (He, Ne, A ,….)
Cv = 3/2 R for wide range of temperature
Cp = 5/2 R for wide range of temperature
γ = 5/3 for wide range of temperature
(3) For diatomic gases (H2, O2, N2, NO, CO ,Air ,….)
Cv = 5/2 R for ordinary temperature and increase as the temperature raised
Cp = 7/2 R for ordinary temperature and increase as the temperature raised
γ = 7/5 for ordinary temperature and decrease as the temperature raised
(4) For polyatomic gases (NH3, CH4, Cl2, CO2,….)
Cp, Cv and g vary with temperature and the variation being different for each gas
Exercise
Using the same principle for u=f(T,v) find similar relation for u=f(p,v) & u=f(p,T) using partial differential equation.
استخدم تعريف معامل الانضغاط عند ثبوت درجة الحرارة
معادلة الحالة خلال عملية اديباتيكية
Gas equation during adiabatic process
العملية الأديباتيكية هي تلك التي لا يكون فيها انسياب للطاقة الحرارية من أو إلى النظام. فإذا افترضنا أن غاز يتمدد أديباتيكلي في مكبس معزول حرارياً لنضمن ان التغير في كمية الحرارة dQ يساوي صفر.
باستخدام القانون الأول للديناميكا الحرارية
dQ = du + dW = 0
But dW= pdv , du = CvdT
therefore Cv dT = -pdv
dT = -pdv/Cv
By differentiating the equation of an ideal gas pv = RT we get
pdv + vdp = RdT
pdv + vdp = R(-pdv/Cv)
pdv + vdp = (Cp – Cv) (-pdv/Cv)
pdv + vdp = -p Cp/Cvdv + pdv
vdp = -p Cp/Cvdv
dp/p + Cp/Cv dv/v = 0
let Cp/Cv = γ
Ln p + Ln vγ = K (where k is a constant)
pvγ = constant
وهذه معادلة الحالة للغاز المثالي في عملية اديباتيكية
الشغل المبذول خلال عملية اديباتيكية
The work done in adiabatic process
لحساب الشغل المبذول خلال عملية اديباتيكية سنقوم بالتعويض في المعادلة العامة للشغل بمعادلة الحالة للغاز المثالي في عملية اديباتيكية.
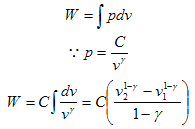
وبما أن pvγ = constant فهذا يعني أن
p2v2γ= p1v1γ = constant = C
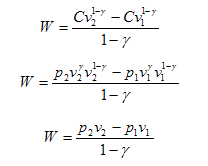
وهذه معادلة الشغل المبذول خلال عملية اديباتيكية
Exercise
By using these relation pvϒ = constant, pv = nRT Prove that
(1) ![]()
(2) ![]()