محاضرة 12 فيزياء حديثة

الوصف الكمي لجسيم محصور في صندوق The Quantum description of a confined particle: إذا افترضنا جسيم محصور في صندوق ذو بعد واحد وأن كمية حركة الجسيم محددة بدقة أي أن Δp_x=0 فإن من مبدأ هيزنبيرج للشك فإن 

Δx=0 , Δλ=0

دعنا نفترض أن الموجة المصاحبة لجسيم محصور في صندوق بالكيفية التي تنحصر فيها الموجة الموقوفة على وتر مشدود.  وأن الجسيم المحصور بتحرك بحرية ذهاباً وإياباً على استقامة محور x وأنه يقابل جدار صلب عند كل من x=0 وx=L.

من وجهة نظر الميكانيكا الموجية فإن احتمالية وجود هذا الجسيم تساوي صفر خارج هذه الحدود وبهذا فإن الدالة الموجية ψ والتي مربعها يمثل الاحتمالية لابد أن تساوي صفر لقيم x أقل من صفر و x أكبر من L. والشروط الحدية هي:

V(x) = 0  for    0 < x < L

V(x) = ∞ for    0 > x < L

ψ(x) = 0  for    0 ≤ x ≤ L

الدالة الموجية التي تحقق هذه الشروط الحدية هي وحدها دون غيرها المتاحة لتمثيل هذه المسألة وحيث أن كمية الحركة التي يحملها الجسيم ثابتة في جميع أنحاء الحيز المذكور فإن λ سوف تكون معلومة القيمة ولذلك سوف تمثل الجسيم بموجة جيبية تحقق الشروط الحدية وعليه فإن الأطوال الموجية المتاحة هي تلك التي تمتلك عدد صحيح من أنصاف الأطوال الموجية في الحيز من x=0 إلى x=L أي أن:

L = n λ/2

حيث أن n عدد صحيح يأخذ القيم 1 , 2 , 3, …………وλ هو الطول الموجي للموجة المصاحبة للجسيم

يوضح الشكل ادناه ثلاثة مستويات يمكن ان يأخذها الجسيم المحصور في صندوق وشكل الدالة الموجية لكل مستوى بحيث تحقق الشروط الحدية وهذه الموجة تسمي موجة موقوفة standing wave حيث أن سعة الموجة عند x=0 وx=L تساوي صفر، ومربع هذه الموجة يحدد أحتمالية تواجد الجسيم في الصندوق لكل مستوى. ففي المستوى الأول والذي يسمى المستوى الأرضي ground state تكون الإحتمالية لتواجد الجسيم أكبر ما يمكن عند منتصف الصندوق x=L/2

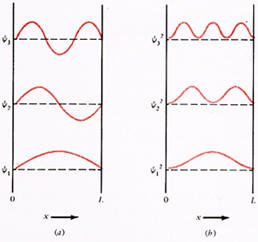
لاحظ هنا أن الشروط الحدية للمسألة وتطبيقها على الدالة الموجية ψ أدت إلى وجود مستويات محددة لتواجد الإلكترون وهذا يعني أن الجسيم مكمم وسنجد أن هذا التكميم موجود في الطاقة التي يمتلكها الجسيم في داخل الصندوق..

إيجاد طاقة كل مستوى

إذا كانت هناك اطوال موجية محدد للجسيم فإن كمية حركة الجسيم ستكون محددة أيضاً وحيث أن العلاقة بين الطول الموجي وكمية الحركة هي

p = h/λ

ولحساب طاقة الحركة للجسيم والتي تساوي الطاقة الكلية للجسيم لأن طاقة الوضع تساوي صفر داخل الصندوق.

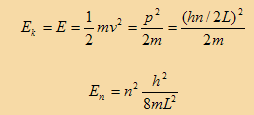
حيث m كتلة الجسيم وn عدد صحيح فإن الطاقة الكلية للجسيم ستكون مكممة وتأخذ القيم الموضحة في الشكل المقابل.

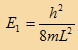      (1)

E_n = n² E₁          (2)

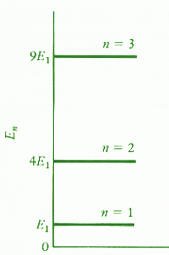
ومقدار الطاقة في ادني مستوى هو E₁ يعرف باسم ground state وتكون الطاقة للمستويات الأعلى هي عبارة عن مربع n في قيمة الطاقة للمستوى الأدنى.

Example

Find the possible values of the energy and speed for the following particles confined to a one-dimensional box:

(a) an electron of mass 9.1×10^-31 kg constrained to move back and forth within an atomic distance L = 4Å;

(b) a relatively large object of 9.1 mg constrained to move along the axis with L=4 cm.

Solution

(a) substituting in equation (1) gives the ground state energy

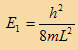
   E₁ = 3.7×10^-19J = 2.3 eV

وتكون قيم مستويات الطاقة الأخرى المسموحة للإلكترون هي:

E_n = n² E₁   or   4E₁, 9E₁, 16E₁, ……..

أما السرعات التي يمتلكها الإلكترون فتحسب على النحو التالي:

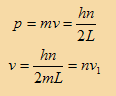
وبحساب اقل سرعة v₁

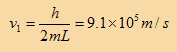
(b) substituting in equation (1) for the large particle

     E₁ = 2.3×10^-42 eV

وهذا مقدار صغير جداً !!

يوضح الشكل التالي مستويات الطاقة في الحالتين ونلاحظ بوضوح تكميم مستويات الطاقة للإلكترون بينما لا نلاحظ التكميم للجسيم المادي الكبير نسبياً حيث تبدو الطاقة متصلة. ولهذا السبب فإننا لا نلاحظ التكميم إلا على الجسيمات المتناهية في الصغر مثل الإلكترون.

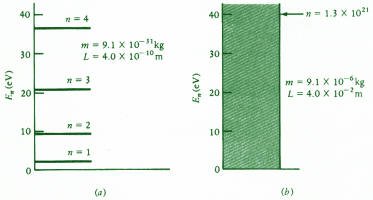
أما السرعات التي يمتلكها الجسيم فتحسب على النحو السابق وتكون السرعة v₁

v1 = 9.1×10^-28m/s

يمكن اعتبار الجسيم ساكن !!

ارجو المساهمة في هذه الحملة