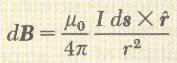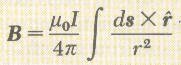محاضرة 5 مغناطيسية وتيار متردد
قانون بيوت سافارت وقانون امبير والفيض المغناطيسي
قانون بيوت سافارت وقانون امبير والفيض المغناطيسي: درسنا في المحاضرات السابقة تعريف المجال المغناطيسي وخصائصه وتأثيره على الشحنة المتحركة الذي يجعل الشحنة تأخذ مساراً دائرياً وتأثيره على سلك يمر به تيار كهربي بقوة وعلى ملف يمر به تيار مما يؤثر عليه بازدواج، ولم نتعرض إلى دراسة مصدر المجال المغناطيسي وكيفية حسابه وفي هذه المحاضرة سوف ندرس قانونين من القوانين التي تتعامل مع هذه الاموضوع القانون الأول يدعى قانون بيوت سافارت Biot Savart Law والقانون الثاني هو قانون امبير Ampere’s Law. وهذين القانونين يناظران قانونين سبق وان درست في الفيزياء العامة 2 وهما قانون كولوم وقانون جاوس لحساب المجال الكهربي.
قانون بيوت سافارت Biot Savart Law
بعد اكتشاف التأثير المغناطيسي عام 1819 بواسطة العلم اوستد Oersted لسلك يمر به تيار كهربي ويؤثر على ابرة مغناطيسية موضوعة بالجوار. قام العالمين بيوت وسافارت بعدة تجارب لايجاد العلاقة بين التيار المار في سلك والمجال المغناطيسي الناتج عنه عند اية نقطة في الفراغ. وقد توصلو إلى الحقائق العملية التالية:
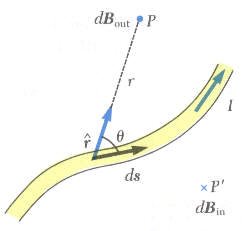
- أن متجه المجال المغناطيسي dB لعنصر صغير من السلك طوله ds عند نقطة P في الفراغ تكون دائما عمودية على كلاً من العنصر ds ومتجه الإزاحة r الذي يتجه من عنصر السلك ds إلى النقطة P.
- يتناسب مقدار المجال المغناطيسي dB عكسيا مع مربع المسافة r2.
- يتناسب مقدار المجال المغناطيسي dB طرديا مع مقدار التيار المار في السلك.
- يتناسب مقدار المجال المغناطيسي dB طرديا مع sinθ حيث أن الزاوية θ هي الزاوية المحصورة بين متجه الازاحة r والعنصر من السلك ds.
- هذه النتائج العملية يمكن تلخيصها في قانون بيوت سافارت
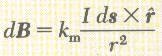
where the constant km = 10-7Wb/A.m (km=υo /4π)
υo is the permeability of the free space. υo = 4πx10-7Wb/A.m
| قانون بيوت سافارت للمجال المغناطيسي النتاج عن عنصر صغير ds من سلك |
|
لاحظ أن القانون السابق يعطي قيمة المجال المغناطيسي الناشئ عن عنصر صغير من السلك ds ولذلك يجب اجراء عملية التكامل للحصول على قيمة المجال المغناطيسي الناتج من السلك كله…
| قانون بيوت سافارت للمجال المغناطيسي الكلي الناتج عن سلك طوله L |
|
قانون امبير Ampere’s Law
قانون أمبير هو صياغة أخرى للعلاقة بين التيار والمجال المغناطيسي الناشئ عنه في صورته التكاملية ويستخدم في حل المسائل التي تحتوي على درجة عالية من التماثل ويأخذ قانون امبير الصورة التالية:
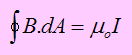
وهذا يعني أن التكامل على مسار مغلق يحيط بالسلك الذي بمر له التيار يساوي قيمة التيار في ثابت السماحية في الفراغ υo.
القوة المغناطيسية المتبادلة بين موصلين يمر بهما تيار كهربي
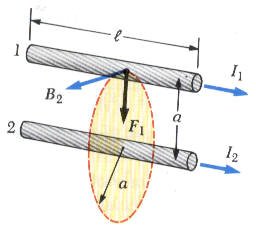
تعلمنا من المحاضرات السابقة أن كل سلك موصل يمر به تيار ينشئ حوله مجالاً مغناطيسياً وأن لكل مجال مغناطيسي قوة مغناطيسية تؤثر على سلك يمر به تيار ولهذا اذا وجد سلكين موصلين كما في الشكل المقابل ويمر بكل منهما تيار كهربي I1 و I2 فإن المجال المغناطيسي B2 الناشئ عن التيار الثاني يؤثر بقوة مقدارها F1. يمكن التعبير عن القوة التي يؤثر بها موصل على اخر كما في الخطوات التالية:
لنعتبر المجال المغناطيسي الناشئ عن السلك 2 والتي تعطى قيمته بالمعادلة التالية:
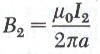
يقع السلك الثاني في المجال المغناطيسي للسلك الثاني والذي يبعد عنه مسافة a كما في الشكل وبالتالي لإن قوة مقناطيسية F1 تعطى بالمعادلة التالية:
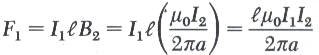
والقوة لكل وحدة اطوال تعطى بالعلاقة التالي:
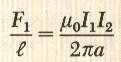
ملاحظة:
تكون القوة بين السلكين قوة تجاذبية إذا كان التيار في السلكين في نفس الأتجاه وتكون القوة المتبادلة قوة تنافرية إذا كان التيار في السلكين في عكس الأتجاه. استخدم قاعدة فلمنج لليد اليمنى للتحقق من ذلك….
من هنا يمكن تعريف الأمبير (وحدة التيار)
حيث أنه يعرف على انه اذا كان هناك سلكين موصلين طويلين والمسافة بينهما 1متر يحملان نفس قيمة التيار وكانت القوة المتبادلة بينهما تساوي 2×10-7N/m فإن قيمة التيار تساوي 1 امبير.
كما يمكن تعريف الكولوم (وحدة الشحنة)
إذا وجد موصل يحمل تيار مقداره 1 امبير فإن الشحنة التي تتدفق خلال الموصل في الثانية الواحدة هي الكولوم.
الفيض المغناطيسي
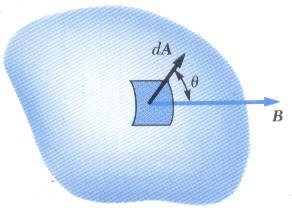
الفيض المغناطيسي وكما عرف الفيض الكهربي يمكن تعريف الفيض المغناطيسي على أنه عدد الخطودط المغناطيسية التي تعبر وحدة المساحات العمودية. افترض أن dA عبارة عن عنصر مساحة من سطح غير منتظم كما في الشكل المقابل، فالفيض المغناطيسي هو عبارة عن عدد الخطوط والذي يعبر عنه بشدة المجال المغناطيسي B مضروب في المساحة العمودية dA.
ويرمز للفيض المغناطيسي بالرمز Fm
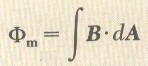
![]()
حيث أن dA هو متجه المساحة وقيمته تعطي مقدار المساحة واتنجاهه يكون دائما عموديا على المساحة.
ملاحظة
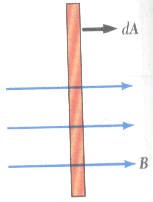
يكون قيمة الفيض المغناطيسي مساوياً للصفر إذا كانت الزاوية المحصورة بين المجال المغناطيسي ومتجه المساحة تساوي 90 درجة وذلك لأنه في هذه الحالة لا توجد خطوط مجال مغناطيسية تخترق المساحة.
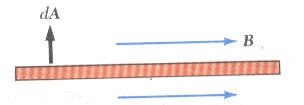
بينما تكون قيمة الفيض المغناطيسي اكبر ما يمكن عندما تكون الزاوية المحصورة بين المجال المغناطيسي ومتجه المساحة تساوي 0 أو 180 درجة وهنا أما أن يكون الفيض المغناطيسي موجباً أو سالباً.
إذا كان الفيض المغناطيسي موجياً فهذا يشير إلى ان خطوط المجال المغناطيسي في اتجاه الخروج من السطح أما اذا كان اشارة الفيض المغناطيسي سالبة فهذا يشير إلى ان خطوط المجال المغناطيسي داخلة على السطح.
| في هذه الحالة الفيض المغناطيسي يساوي صفر لأن المتجه dA عمودي على متجه المجال B |
|
| في هذه الحالة الفيض المغناطيسي يساوي BA لأن المتجه dA في نفس اتجاه على متجه المجال B والزاوية المحصورة تساوي صفر |
|
وحدة الفيض المغناطيسي هي الويبر
Wb = 1 T.m2