معادلة شرودينجر Schrödinger Equation: نعلم أن أي موجة تنتشر في اتجاه واحد x يمكن وصفها من خلال المعادلة التفاضلية التالية:
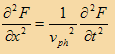 (1)
(1)
حيث F تمثل الدالة الموجية التي تعتمد على المكان x والزمن t. والسرعة vph2 تمثل سرعة الموجة (phase speed), فإذا كنا نتحدث على موجة صوتية مثلاً تنتشر في الهواء فإن الدالة الموجية F هي مقدار التغير في التضاغط والتخلخل في جزيئات الهواء والسرعة vph هي سرعة الصوت في الهواء وإذا كانت موجة ضوء فإن الدالة الموجية F هي التغير في المجال الكهربي والمغناطيسي والسرعة هي سرعة الضوء.
في حالة وصف جسيم بدالة موجية فإن مربع الدالة الموجية يعبر عن احتمالية رصد الجسيم في الفراغ في وحدة الزمن. وسوف نرمز لهذه الدالة الموجية بالرمز Ψ.
وحيث أن الدالة الموجية متغيرة في كل من المكان والزمان لذا سنفترض أنها تأخذ الصورة التالية:
Ψ(x,t) = ψ(x) f(t) (2)
عند صياغة معادلة شرودنجر نفترض نظام مكون من جسيم يتحرك في بعد واحد x وينتشر كموجة وان هذا الجسيم يتفاعل مع ما يحيط به ومرتبط به من خلال دالة الجهد V وله طاقة كلية E ثابتة وسوف نفترض أن التردد معروف بدقة f=h/E لذا فإن الدالة f تكون دالة جيبية على النحو التالي:
f(t) = cos 2πf t (3)
بالتعويض في المعادلة (1) بالدالة الموجية في المعادلة (2) نحصل على
![]()
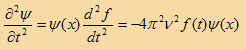
بالتعويض في المعادلة (1) نحصل على
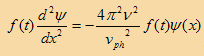
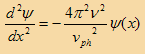
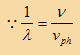
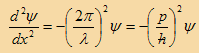 (4)
(4)
إذا كان الجسيم وكتلته m موجود في وسط له جهد V فتكون الطاقة الكلية E للجسيم والوسط هو مجموع طاقة الحركة Ek وطاقة الوضع الممثلة في الجهد V.
![]()
![]() (5)
(5)
بالتعويض في المعادلة (4) من المعادلة (5)
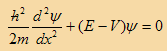 (6)
(6)
وهذه معادلة شرودينجر في بعد واحد والتي تفترض أن الجسيم ينتشر على شكل موجة وتسمى بالمعادلة الموجية وحيث أن الجسيم يتفاعل مع المحيط الموجود به من خلال الجهد V.
باستخدام معادلة شرودينجر على جسيم مرتبط بجهد V أي أن القوة التي يؤثر بها الوسط على الجسيم المرتبط معروفة يمكن إيجاد الدالة الموجية ومستويات الطاقة المسموحة وكمية الحركة. وحيث أن مربع الدالة الموجية يعبر عن احتمالية تواجد الجسيم في مكان x في وحدة الزمن فإن الحل المقبول للدالة الموجية ψ يجب أن يحقق الشروط الحدية التي يفرضها الجهد V وهذه الشروط الحدية سوف تؤدي إلى تكميم الطاقة للجسيم أي أن تكون هناك قيم محدد فقط للطاقة مسموحة.
ولتوضيح هذا سوف نطبق معادلة شرودينجر على المثال السابق لجسيم في صندوق جهد لانهائي.
جسيم في صندوق جهد لانهائي ذو بعد واحد Particle in one dimensional potential well of infinite height
من أسهل التطبيقات على معادلة شرودينجر هو حل مشكلة جسيم موجود داخل صندوق ذو بعد واحد L وجدار الصندوق تمثل جهد V لانهائي بحيث لا يمكن للجسيم ان يفلت من هذا الجهد وبالتالي فإن الجسيم سيحدد وجوده في المسافة بين x=0 و x=L. حيث يتحرك بحرية في هذا المدى بجهد يساوي صفر وتكون التصادمات بين الجسيم وجدار الصندوق هي تصادمات مرنة لا يفقد فيها الجسيم طاقة.

بالتعويض عن قيمة الجهد V=0 في معادلة شرودنجر نحصل على
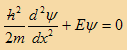 (7)
(7)
بإعادة ترتيب المعادلة على الشكل التالي:
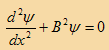 (8)
(8)
حيث أن
![]()
حيث أن الصندوق يمثل الجهد المطبق على الجسيم واعتبر أن جدار الصندوق ذات ارتفاع لانهائي بحيث لا يمكن للجسيم أن يتواجد خارج الصندوق لذا فإن الشروط الحدية هي:
V(x) = 0 for 0 < x < L
V(x) = ∞ for 0 > x < L
y(x) = 0 for 0 ≥ x ≥ L
والحل الذي يحقق المعادلة التفاضلية (7) يجب أن يكون متوافق مع الشروط الحدية السابقة أي أن
ψ(0) = 0 & ψ(L) = 0
والحل المناسب الذي يحقق تلك الشروط هو
ψ(x) = A sin Bx
نلاحظ أن الشرط ψ(0) = 0 محقق، ولكي يصبح الشرط الثاني ψ(L) = 0 محقق فإن BL=nπ حيث n عدد صحيح وبالتعويض عن B نحصل على
![]()
وعليه تكون الطاقة للجسيم داخل صندوق الجهد هو
![]()
وتكون الدالة الموجية له هي
![]()
وهذه نفس النتائج التي حصلنا عليها في السابق والتي توضح أن الطاقة المسموحة للجسيم مكممة.



