فرضية بوهر Bohr’s Postulates
كل النتائج التي اكتشفها العلماء حول الطيف الذري وفرضيات التي وضعها العالمان تومسون ورذرفورد كانت متوفرة للعالم بوهر وكان على نموذجه الذي وضعه ان يقدم حلاً للمشاكل التي واجهت النموذجين السابقيين للذرة من حيث تفسير استقرار الذرة وتفسير الطيف الكهرومغناطيسي المنبعث من ذرة الهيدروجين.
في العام 1913 تمكن العالم بوهر Nile Bohr من وضع تصور ناجحاً لتركيب الذرة، اعتمد نموذج بوهر للذرة على الفرضيات التالية:
(1) الألكترون يدور حول النواة في مدار دائري تحت تأثير قوة التجاذب الكهربي (قوى كولوم) بين النواة الموجبة الشحنة والإلكترون السالب الشحنة.
(2) المدار الذي يسلكه الإلكترون حول النواة هو المدار الذي يكون عزم العزم الزاوي orbital angular momentum L تساوي عدد صحيح من ثابت بلانك مقسوم على 2p أي
L = nh/2p where n = 1,2,3, …….(1)
(3) بالرغم من أن الإلكترون يتحرك بعجلة في مداره الدائري حول النواة إلا ان في هذه المدارات المحددة بالفرضية الثانية فإن الإلكترون لا يشع اي طيف كهرومغناطيسي كما تنص النظرية الكلاسيكية وبالتالي فإن الطاقة الكلية للإلكترون تبقى ثابتة.
(4) ينبعث الطيف الكهرومغناطيسي إذا انتقل الإلكترون من مدار طاقته Ei إلى مدار طاقته Ef ويكون طاقة الفوتون المنبعث على شكل طيف كهرومغناطيسي تساوي فرق الطاقة بين المستويين
hv = Ei – Ef (2)
شرح فرضيات نموذج بوهر
(1) ترتكز الفرضية الأولى على تثبيت أن الذرة مكونة من نواة والإلكترون يدور حولها كما جاء في نموذج رزرفورد.
(2) تأتي الفرضية الثانية معتمدة على مبدأ التكميم وهذه اول فرضية تدخل مبدأ الكم في نموذج تركيب الذرة حيث حددت الفرضية ان المدارات التي يمكن ان يسلكها الإلكترون حول النواة هي تلك المحددة بالمعادلة (2). وهذا التكميم سوف يؤدي إلى تكميم الطاقة الكلية للإلكترون. وتجدر الإشارة هنا إلى ان العالم بلانك قد اكتشف مسبقاً ان الجسم الذي يتحرك حركة توافقية بسيطة تحت تأثير قوة استرجاعية فإنه يمتلك طاقة مكممة تعطى بالعلاقة E=nhv وهنا للمقارنة نجد ان بوهر قد استفاد من هذه النتيجة حيث اعتبر ان طاقة الإلكترون مكممة نظراً مع أن الإلكترون يدور تحت تأثير قوة كولوم.
(3) أعتبر بوهر ان النظرية الكلاسيكية غير مطبقة في هذه الحالة التي يدور فيها الإلكترون حول النواة في مدارات مكممة وأنه لا يبعث طيف كهرومغناطيسي حتى يفسر سبب استقرار الذرة.
(4) اعتمدت الفرضية الرابعة على فرضية أينشتين في ان تردد الفوتون يساوي طاقته مقسومة على ثابت بلانك.
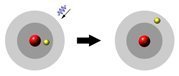 | 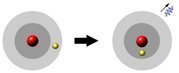 |
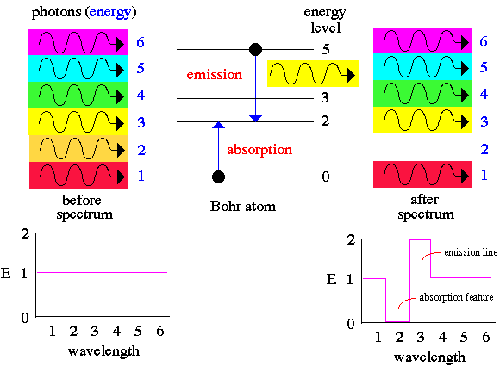
| الكترون يمتص طاقة فوتون لينتقل من مدار إلى مدار ذو طاقة أعلى | الكترون ينتقل من مدار ذو طاقة عالية إلى مدار ذو طاقة اقل وينطلق فوتون يحمل فرق الطاقة بين المستويين |
من هذه الفرضيات نرى ان بوهر قد دمج النظرية الكلاسيكية من نظرية الكم في اعتباره ان الإلكترون يتحرك في مداره الدائري ويطيع فرضيات النظرية الكلاسيكية بينما في تكميم المدار وانبعاث الطيف الكهرومغناطيسي فإن ذلك لا يتفق مع النظرية الكلاسيكية. سوف يتضح من خلال هذه المحاضرات إنه لا يمكن ان نستخدم النظرية الكلاسيكية في حالة التعامل مع الإجسام الدقيقة مثل الذرة.
نموذج بوهر
إن نجاح نموذج بوهر يعتمد على مدى مطابقة النتائج المستخلصة من فرضياته مع نتائج التجارب العملية، وهنا سوف نقوم باشتقاق العلاقات النظرية المعتمدة على فرضيات بوهر ومقارنتها مع النتائج العملية.
نفترض ذرة تحتوي على نواة بشحنة Ze وكتلة M وإلكترون شحنته e وكتلته m وهنا نفترض ان كتلة الإلكترون مهملة بالنسبة لكتلة النواة وبناءً عليه نفرض ان النواة ثابتة في الفراغ. من قانون الحفا على بقاء الإلكترون في مداره فإنه يقع تحت تأثير قوتين متساويتين في المقدار ومتعاكستين في الأتجاه (قوة كولوم وقوة الطرد المركزي).
ملاحظة: يمكن تطبيق ما يلي على ذرة الهيدروجين حيث Z=1 أو ذرة الهيليوم انتزع منها الكترون (هيليوم احادي التأين) حيث Z=2 أو ذرة ليثيوم انتزع منه الكترونيين (ليثيوم ثنائي التأين) Z=3.
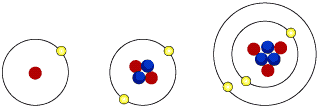
H He Li
إيجاد نصف القطر والسرعة للإلكترون حول النواة
![]() (3)
(3)
حيث أن v هي سرعة الإلكترون في مداره حول النواة و r نصف قطر المدار. وباستخدام الفرضية الثانية لبوهر المتعلقة بالعزم الزاوي للإلكترون حول النواة.
L =mvr = nh/2p (4)
بالتعويض عن v من المعادلة (4) في المعادلة (3) نحصل على
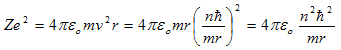
وبالتالي يكون نصف القطر للمدار
![]() (5)
(5)
وسرعة الإلكترون في المدار هي
![]() (6)
(6)
where n = 1,2,3, ………
إن تكميم العزم الزاوي المداري للإلكترون حول النواة ادى إلى تكميم المدارات الممكنة للإلكترون حول النواة من خلال تحديد نصف قطر المدارات الممكنة للالكترون ان يتواجد بها ونجد ان نصف قطر المدار يتناسب طرديا مع مربع العدد الكمي n
وبالتعويض في المعادلة (5) عن n=1 يمكن حساب قيمة نصف القطر للمدار الأول للإلكترون حول النواة لذرة الهيدروجين حيث Z=1 فإن نصف القطر يساوي
r = 5.3×10-11m =0.5A
وهذه القيمة مقبولة لتحديد نصف قطر الذرة وهي في حدود القيمة التي اعتمدها رزرقورد في نموذجه للذرة عندما قدر نصف قطر النواة.
وبالتعويض في المعادلة (6) يمكن حساب سرعة الإلكترون حول النواة في المدار الأول n=1لذرة الهيدروجين وبالتعويض عن الثوابت في المعادلة نجد أن سرعة الإلكترون تساوي
v =2.2×106m/sec
وهذه هي اكبر سرعة للالكترون حول النواة لان السرعة تتناسب عكسياً مع العدد الكمي للمدار. وعندما نتحدث عن ذرات لها عدد ذري اكبر من ذرة الهيدروجين Z>1 فإن السرعة تصبح قريبة من سرعة الضوء وهنا يكون نموذج بوهر غير متحقق لتلك الذرات لانه لم تتعامل مع سرعات قريبة من سرعة الضوء.
إيجاد الطاقة الكلية للالكترون في المدار حول النواة
لحساب الطاقة الكلية للإلكترون في اي من المدارات المسموح بها حول النواة فإننا سنقوم بجمع طاقة الوضع الناتجة عن التجاذب بين شحنة النواة الموجبة وشحنة الإلكترون السالبة مع افتراض ان طاقة الوضع تساوي صفر عندما يكون الإلكترون في الملانهاية، مع طاقة حركة الإلكترون.
The potential energy ![]()
الاشارة السالبة لطاقة الوضع تشير إلى أن القوة المتبادلة بين النواة والإلكترون هي قوة تجاذب وان هناك شغل سالب يبذل لاحضار الإلكترون من المالانهاية إلى مداره حول النواة.
The kinetic energy
حيث تم استخدام المعادلة (3) للتعويض عن mv2
The total energy ![]()
بالتعويض عن قيمة r من المعادلة (5) في معادلة الطاقة نحصل على
![]() (7)
(7)
where n = 1,2,3,…….
ومن المعادلة (7) نستنتج أن الطاقة أيضا مكممة.
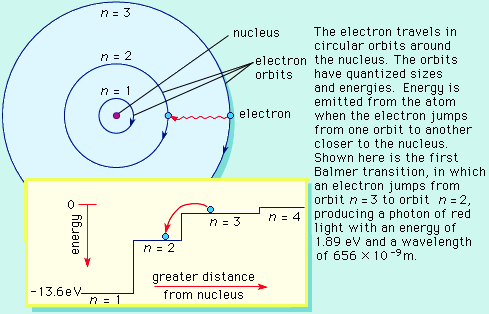
المخطط التالي يوضح المعلومات الواردة في المعادلة (7) والتي توضح مستويات الطاقة المكممة لذرة الهيدروجين بناءً على المعادلة (7) والقيم الواردة على يمين المخطط تبين العدد الكمي n والقيم على الجانب الأيسر توضح قيمة الطاقة المقابلة لكل مستوى طاقة من حسابها بالمعادلة (7) وذلك بوحدة الجول وبوحدة الإلكترون فولت. لاحظ ان اجنى مستوى للطاقة هو المستوى ذو العدد الكمي الأصغر n=1 وكلما زادت n كلما كانت الطاقة الكلية اقل سالبية وتكون الطاقة الكلية مساوية للصفر عندماتؤول n إلى المالانهاية. إن أقل مستوى طاقة هو الأكثر استقراراً بالنسبة للإلكترون وهو المستوى n=1 في حالة ذرة الهيدروجين.

The energy level diagram for the hydrogen atom
حيث ان الإلكترون في الحالة العادية يكون في أدنى مستوى للطاقة وفي ذرة الهيدوجين يكون فى المستوى n=1 وبالتالي لانتزاع الإلكترون من نواة ذرة الهيدروجين فإنه يجب أن نتغلب على طاقة ارتباطه بالنواة وهي طاقة المستوى الموجود به وتحرير الإلكترون يجعل الذرة ذات شحنة موجبة وهنا تسمى أيون.
لحساب طاقة الإلكترون في المستوى الأول نعوض عن n=1 في المعادلة (7) كما يلي:
![]()
![]()
![]()
وهذه هي قيمة الطاقة للمستوى الأول وهي طاقة ربط الإلكترون بالنواة والتي تسمى Binding energy
اما طاقة المستويات الإخرى فيمكن حسابها استناداً إلى قيمة الطاقة في المستوى الأول من العلاقة التالية:
![]()
E2 = -3.39eV, E3 = -1.51eV, E4 = -0.85eV, ………..
إيجاد تردد الإشعاع الكهرومغناطيسي الناتج عن انتقال الإلكترون بين مستويات الطاقة
تنص الفرضية الرابعة لبوهر على أن الطيف الكهرومغناطيسي ينبعث من الذرة عندما ينتقل الإلكترون من مدار ni إلى مدار nf وذلك حسب التالي:
hv = Ei – Ef
بالتعويض عن كلاً من Ei و Ef باستخدام المعادلة (7) نحصل على
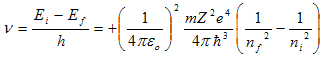
وباستخدام مقلوب الطول الموجي (الرقم الموجي) Wave Number k
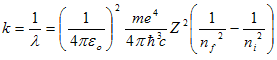
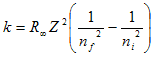 where
where 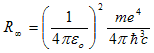 (8)
(8)
تعد المعادلتان (7) و (8) اهم استنتاجين لنموذج بوهر وباستخدام هاتين المعادلتين يمكن شرح الطيف الكهرومغناطيسي المنبعث من ذرة الهيدروجين.
(1) إن المستوى الأول للطاقة n=1 وهو أدنى مستوى للطاقة يسمى Ground state.
(2) عند اثارة ذرة الهيدروجين باستخدام على سبيل المثال التفريغ الكهربي electric discharg فإن الإلكترون في المستوى n=1 سوف يكتسب طاقة نتيجة التصادمات فينتقل إلى مستوى طاقة أعلى n>1 وهنا تصبح ذرة الهيدروجين مثارة excited state.
(3) تتخلص الذرة من حالة الإثارة عن طريق انبعاث فوتون يحمل فرق الطاقة بين المستويين. ويمكن ان يتم الإنتقال من خلال سلسلة من الإنتقالات حتى الوصول إلى المستوى n=1وفي كل مرحة إنتقال إلى مستوى طاقة أقل ينطلق فوتون. فمثلاً إذا اثير الإلكترون إلى المستوى n=7 فإنه ينتقل مثلاً إلى المستوى n=4 ثم ينتقل إلى المستوى n=2 ثم إلى المستوى n=1، وفي هذه الحالة نحصل على ثلاثة خطوط طيفية لها طول موجي يمكن حسابه من المعادلة (8) بالتعويض عن ni=7 و nf=4 للخط الطيفي الأول والخط الثاني ni=4 و nf=2 والخط الثالث ni=2 و nf=1.
(4) يمكن ان تحدث الانتقالات الطيفية كل مستويات الطاقة من مستوى الطاقة الأعلى ni إلى مستوى الطاقة الأقل nf وفي حالة ذرة الهيدروجين Z=1 يمكن استخدام المعادلة (8) لحساب كافة الانتقالات الطيفية التي يمكن تجميعها في سلسة من الخطوط الطيفية حسب مستوى الطاقة الأدنى nf الذي تؤول إليه كل الانتقالات. فمثلا الانتقالات التي تنتهي إلى المستوىnf=1 تسمى Lyman series أما الانتقالات إلى إلى المستوى nf=2 فتسمى Balmer seriesوالانتقالات إلى المستوى nf=3 تسمى Paschen series والانتقالات إلى nf=4 تسمى Brackett series والانتقالات إلى nf=5 تسمى Pfund series. وهذه التسميات تعود إلى العلماء الذين اكتشفوا هذه الخطوط الطيقية لذرة الهيدروجين. وفد وجدت قيم الأطوال الموجية التي نحصل عليها من المعادلة (8) متفقة مع النتائج العملية لطيف الهيدروجين كما في الشكل التالي:
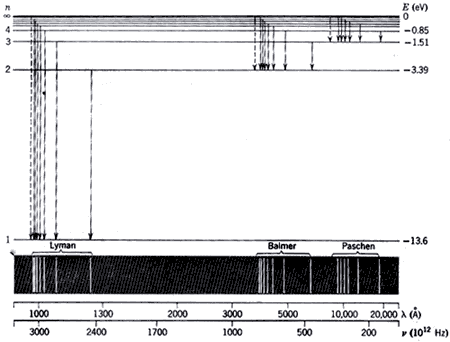
لاحظ أن الخطوط الطيفية التابعة لمجموعة Lyman series هي ذات طاقة فوتون الأعلى وهي لهذا السبب تكون في منطقة الفوق بنفسجية من الطيف الكهرومغناطيسي. وان الانتقال من المستوى إلى المستوى n=1 هو الخط الطيفي ذو الطاقة الأعلى في المجموعة والانتقال من المستوى ni=2 إلى nf=1 هو الأقل طاقة في مجموعة Lyman series.
ملاحظة: كما لاحظنا اتفاق التائج العملية في حالة الانبعاث الإشعاعي Emission مع الحسابات الناتجة عن فرضية بوهر فإنه أيضا في حالة الامتصاص Absorption تتفق ايضا ولكن فقط في حالة الامتصاص لايمكن ان نلاحظ عمليا سوى مجموعة Lyman لان الامتصاص يعتمد على الالكترونات في مستوى الطاقة الأدني وعند درجات الحرارة العادية تكون كل الإلكترونات في المستوى n=1.
الفرق بين الانبعاث والامتصاص للفوتون



