محاضرة 6 ديناميكا حرارية

من خلال النظرية الحركية للغازات سوف نستنتج العلاقة بين الطاقة الحركية للجزيئات والطاقة الداخلية للنظام.  وسوف تزودنا هذه النظرية بالمعنى الفيزيائي لدرجة الحرارة والضغط.

فرضيات النظرية الحركية للغازات
(1) عدد جزيئات الغاز كبير جدا والمسافة بينهم كبيرة، كما إن حجم جزيئات الغاز مهمل بالنسبة لحجم الوعاء الذي يحتويه.
(2) تخضع حركة الجزيئات لقوانين نيوتن للحركة، كما أن حركة الجزيئات حركة عشوائية.
(3) التصادمات بين الجزيئات تصادمات مرنة.
(4) القوة المتبادلة بين الجزيئات مهملة ماعدا القوة الناتجة من التصادمات بين الجزيئات.
(5) الغاز نقي.
(6) يكون الغاز في حالة اتزان حراري مع مع جدار الوعاء الذي يحتويه.

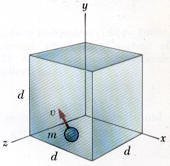
يكون ضغط الغاز ناتجاً من التصادمات المرنة لجزيئات الغاز مع الجدار.  ولهذا فإن الضغط الناتج عن عدد N من جزيئات الغاز تشغل حجم V من وعاء أبعاده d كما في الشكل المقابل.

إذا تحركت احد الجزيئات باتجاه جدار الوعاء بسرعة v وبعد التصادم معه فإنها ترتد في الاتجاه المعاكس ويكون في هذه الحالة مركبة السرعة في احد المحاور سالبة كما في الشكل، حيث أن الجزئ تحرك إلى اليمين ليصطدم بالجدار ويرتد عنه، وبتحليل متجه السرعة v إلى مركباته نجد أن المركبة على محور x تكون إلى اليسار أي في الاتجاه السالب.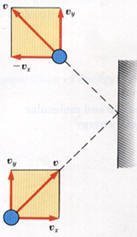

سنقوم بحساب التغيير في كمية الحركة change in momentum للجزئ.

Δp_x = -mv_x – mv_x = -2mv_x

وهذه هي قيمة كمية الحركة التي تعطي للجدار بعد كل تصادم.

لأي جزئ بعمل تصادمين متعاقبين مع نفس الجدار فإنه يجب أن يقطع مسافة وقدرها 2d في فترة زمنية Δt وتكون المسافة التي يقطعها الجزئ في تلك الفترة الزمنية هي v_xΔt.

الزمن بين تصادمين متعاقبين هو

Δt = 2d/v_x

إذا كانت F هي مقدار القوة المتوسطة التي تبذل بواسطة الجزئ على الجدار في فترة زمنية Dt وتسمى الصدمة Impulse والتي تعرف بالتغيير في كمية الحركة.

F Δt = Δp_x = -2mv_x

F = 2mv_x/Δt = 2mv_x/2d/v_x = mv²_x/d

تكون القوة الكلية المؤثرة على الجدار هي مجموع القوى الناتجة من الجزيئات المتصادمة مع الجدار، وللحصول على قيمة الضغط الكلي الناتج فإن

P = F/A = m/dA (v²x₁+v²x₂+v²x₃+….)

وتكون قيمة السرعة المتوسطة هي

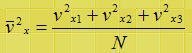
 وحيث أن

  v² = v_x² + v_y² + v_z²

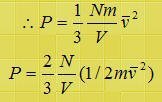
ومن هذه المعادلة نستنتج أن الضغط يتناسب طردياً مع عدد الجزيئات لكل وحدة حجوم ويتناسب طردياً مع طاقة حركة الجزيئات.

التفسير الفيزيائي لدرجة الحرارة
بإعادة كتابة المعادلة السابقة كما في الشكل التالي:

P V = N k T

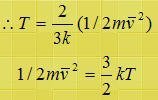
وهذا بعني أن درجة الحرارة هي مقياس لمتوسط طاقة حركة الجزيئات

وحيث أن

وتكون طاقة الحركة الكلية لعدد N من الجزيئات يساوي

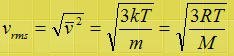
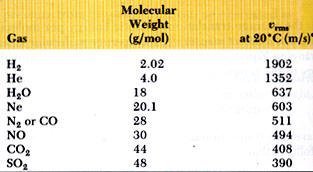
ومن هذه المعادلة نستنتج أن الجزيئات الخفيفة تتحرك بسرعات أكبر من الجزيئات الثقيلة.

يوضح الجدول التالي بعض السرعات لعدد من الجزيئات عند درجة حرارة 20 درجة مئوية.

Example
A tank of volume 0.3m³ contains 2 mole of helium gas at 20^oC.  Assuming the helium behaves like an ideal gas, (a) find the total internal energy of the system.  (b) what is the average kinetic energy per molecule?

Solution
(a) Using equation for n=2mol, R=8.31J/mol.K  and T=293K
                

               E = 7.3x10³J

(b) Using equation for k=1.38x10^-23J/K and T=293K

= 6.07x10^-21J