محاضرة 10 مغناطيسية وتيار متردد
دوائر التيار المتردد Alternating Current Circuits
دوائر التيار المتردد Alternating Current Circuits: سندرس في هذه المحاضرة والمحاضرات القادمة المبادئ الأساسية لدوائر التيار المتردد. حيث سنركز على تأثير التيار المتردد على المقاومة والمكثف والملف. وقد سميت بدوائر التيار المتردد لأن التاير الكهربي يتغير مع الزمن بدالة جيبية كما لا حظنا في فكرة عمل المولد الكهربي والموتور. سنعتمد في تحليل الدائرة الكهربية على قانون كيرشوف لإيجاد علاقة التيار بالجهد الكهربي على كل عنصر من عناصر الدائرة الكهربية.
يمثل مصدر القوة الدافعة الكهربية في الدائرة بالرمز ![]() ويكون فرق الجهد
ويكون فرق الجهد
v = Vm sinωt
Where Vm is the Peak voltage and w is the angular velocity
w = 2πf = 2π/Τ
Where f is the frequency of the source and Τ is the period.
المقاومة في دائرة تيار متردد Resistor in an AC circuit
بتطبيق قانون كيرشوف على الدائرة الموضحة في الشكل والتي تتكون من مقاومة ومصدر تيار متردد.
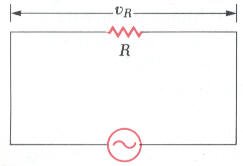
v = vR = Vm sinωt
حيث أن vR قيمة فرق الجهد اللحظي المطبق على طرفي المقاومة وVm القيمة العظمى لفرق الجهد، وتكون قيمة التيار اللحظي
iR = v/R = Vm/R sinωt = Im sinωt
حيث أن Im القيمة العظمى للتيار المار في المقاومة،
Im= Vm/R
تعطى قيمة فرق الجهد اللحظي بدلالة التيار من خلال المعادلة التالية:
vR = ImR sinωt
من المعادلة الأخيرة نستنتج أن كلاً من الجهد والتيار يتغيران بدالة جيبية وبنفس الطور In Phase وهذا كما يوضحه الشكل التالي:
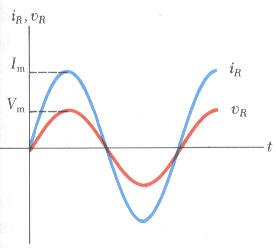
منحنيات الطور Phaseors Diagram
من المناسب الاستعانة بمنحنيات الطور التي توضح علاقة الطور بين التيار وفرق الجهد عند أية لحظة زمنية وذلك بتمثيل التيار بمتجه طوله Im وفرق الجهد بمتجه طوله Vm ويصنع كل متجه زاوية ωt مع المحور الافقي ويكون مسقط المتجهان على المحور الرأسي يمثلا قيمة التيار الحظي وفرق الجهد اللحظي.
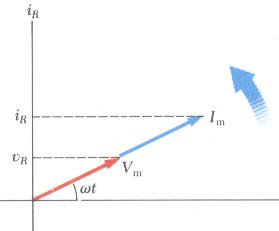
كلا من التيار والجهد لهما نفس الطور Both the current and the voltage are in phase
القدرة الكهربة Power
تعطى القدرة الكهربية بالقلاقة P = i2R وحيث أن التيار المار في الدائرة الكهربية هو تيار متردد فإن تأثيره سيكون مختلف فيما لو عوضنا في المعادلة السابقة عن القيمة العظمى للتيار لأن ذلك لا يدوم إلا لفترة زمنية قصيرة وعليه يجب التعامل من قيمة تعبر عن متوسط قيمة التيار المتردد أو الجهد الكهربي وهذا مايعرف بـ root mean square حيث ان
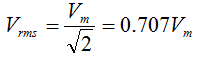 &
& 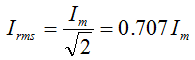
وعليه تعطى القدرة الكهربية بـ Pav=Irms2 R
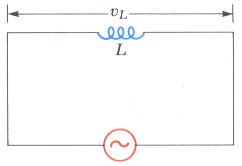
ملف في دائرة تيار متردد Inductor in an AC circuit
بتطبيق قانون كيرشوف على الدائرة الموضحة في الشكل والتي تتكون من ملف ومصدر تيار متردد.
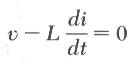

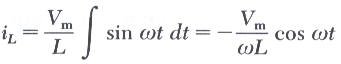
using the trigonometric identity
cos ωt = – sin (ωt-π/2)
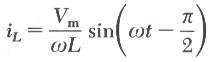
من المعادلة الأخيرة نستنتج أن التيار يتأخر عن الجهد بزاوية مقدارها 90 درجة وهنا يكون الطور بينهما مختلف كما يوضحه الشكل التالي:
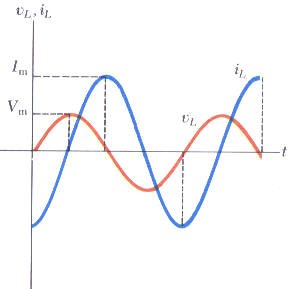
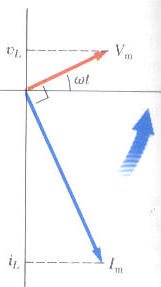
حيث أن Im القيمة العظمى للتيار المار في الملف وتعطى بالعلاقة،
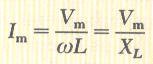
where XL is called inductive reactance
XL= wL
تعطى قيمة فرق الجهد اللحظي بدلالة التيار من خلال المعادلة التالية:
vL = Vm sinωt = ImXL sinωt
مكيف في دائرة تيار متردد Capacitor in an AC circuit
بتطبيق قانون كيرشوف على الدائرة الموضحة في الشكل والتي تتكون من مكثف ومصدر تيار متردد.
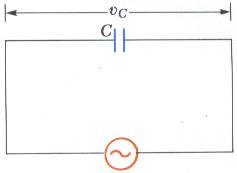
v – vC = 0
v = vC = Vm sinωt
حيث أن vC قيمة فرق الجهد اللحظي المطبق على طرفي المكثف ونعلم أن
vC = Q/C
Q = CVm sinωt
The current iC = dQ/dt
iC = dQ/dt = ωCVm cosωt
using the trigonometric identity
cos ωt = sin (ωt+π/2)
من المعادلة الأخيرة نستنتج أن التيار يتقدم عن الجهد بزاوية مقدارها 90 درجة وهنا يكون الطور بينهما مختلف كما يوضحه الشكل التالي:
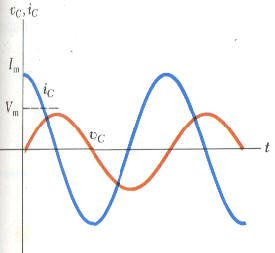
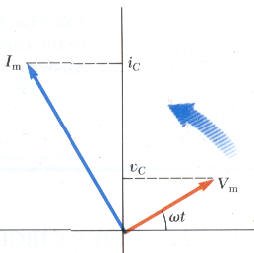
حيث أن Im القيمة العظمى للتيار المار في المكثف وتعطى بالعلاقة،
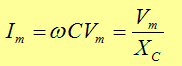
where XC is called capacitive reactance
XC= 1/ωC
تعطى قيمة فرق الجهد اللحظي بدلالة التيار من خلال المعادلة التالية:
vC = Vm sinωt = ImXC sinωt



